题目内容
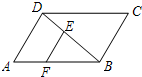（2008•宝山区二模）如图，已知在平行四边形ABCD中，EF∥AD，DE：EB=2：3，EF=6，那么BC的长为10
10
．分析：由四边形ABCD是平行四边形可以得出BC=AD，根据DE：EB=2：3可以求出BE：BD=3：5，再利用三角形相似就可以求出AD的值，从而可以求出BC的值．
解答：解：∵四边形ABCD是平行四边形，
∴AD=BC，
∵EF∥AD，
∴
=
．
∵DE：EB=2：3，设DE=2x，BE=3x，则BD=5x．
∴
=
，
∴
=
∵EF=6，
∴
=
，
∴AD=10，
∴BC=10．
故答案为：10．
∴AD=BC，
∵EF∥AD，
∴
| EF |
| AD |
| BE |
| BD |
∵DE：EB=2：3，设DE=2x，BE=3x，则BD=5x．
∴
| BE |
| BD |
| 3 |
| 5 |
∴
| EF |
| AD |
| 3 |
| 5 |
∵EF=6，
∴
| 6 |
| AD |
| 3 |
| 5 |
∴AD=10，
∴BC=10．
故答案为：10．
点评：本题考查了平行四边形的性质，相似三角形的判定与性质的运用．
练习册系列答案
相关题目
（2008•宝山区二模）甲、乙二人沿相同的路线由A到B匀速行进，A，B两地间的路程为20km．他们行进的路程s（km）与甲出发后的时间t（h）之间的函数图象如图所示．根据图中信息，下列说法中，不正确的是（ ）