题目内容
如图1, ,点
,点 在第二象限内,点
在第二象限内,点 在
在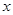 轴的负半轴上,
轴的负半轴上,


小题1:求点 的坐标
的坐标
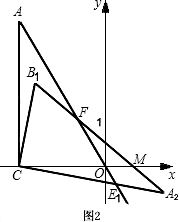
小题2:如图2,将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 到
到 的位置,其中
的位置,其中 交直线
交直线 于点
于点 ,
,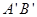 分别交直线
分别交直线 于点
于点 ,则除
,则除 外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);
外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);
小题3:在⑵的基础上,将 绕点
绕点 按顺时针方向继续旋转,当
按顺时针方向继续旋转,当 的面积为
的面积为 时,求直线
时,求直线 的函数表达式.
的函数表达式.
 ,点
,点 在第二象限内,点
在第二象限内,点 在
在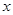 轴的负半轴上,
轴的负半轴上,


小题1:求点
 的坐标
的坐标小题2:如图2,将
 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 到
到 的位置,其中
的位置,其中 交直线
交直线 于点
于点 ,
,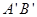 分别交直线
分别交直线 于点
于点 ,则除
,则除 外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);
外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);小题3:在⑵的基础上,将
 绕点
绕点 按顺时针方向继续旋转,当
按顺时针方向继续旋转,当 的面积为
的面积为 时,求直线
时,求直线 的函数表达式.
的函数表达式.小题1:

小题2:

小题3:
 或
或
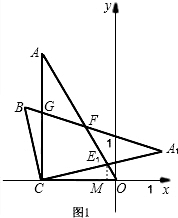
分析:(1)首先在Rt△ACO中,根据∠CAO=30°解直角三角形可以得到OA,OC的长,然后就可以得到点C的坐标;
(2)根据已知条件容易得到△A′EF≌△AGF或△B′GC≌△CEO或△A′GC≌△AEC;
(3)过点E1作E1M⊥OC于点M,利用S△COE1=4和∠E1OM=60°可以求出点E1的坐标,然后利用待定系数法确定直线CE的解析式.此题有两种情况,分别是E在第二或四象限里.
解:(1)∵在Rt△ACO中,∠CAO=30°,OA=4,
∴OC=2,
∴C点的坐标为(-2,0).
(2)△A′EF≌△AGF或△B′GC≌△CEO或△A′GC≌△AEC.
(3)如图1,过点E1作E1M⊥OC于点M.
∵S△COE1=
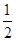 CO?E1M=
CO?E1M=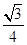 ,
,∴E1M=
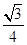 .
.∵在Rt△E1MO中,∠E1OM=60°,则
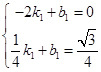 ,
,∴tan60°=
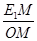 &∴OM=
&∴OM=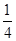 ,
,∴点E1的坐标为(-
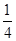 ,
,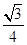 ).
).设直线CE1的函数表达式为y=k1x+b1,
解得
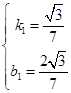 .
.∴y=
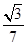 x+
x+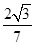 .
.同理,如图2所示,点E2的坐标为(
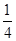 ,
,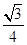 ).
).设直线CE2的函数表达式为y=k2x+b2,则
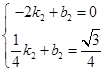 ,
,解得
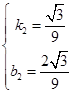 .
.∴y=-
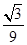 x-
x-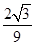 .
.
练习册系列答案
相关题目



 ,∠C=30
,∠C=30 B 2
B 2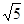 C 4
C 4 D 4
D 4 B.
B.  C
C D
D