��Ŀ����
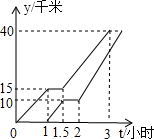 ����������ͬһ����ֱ�Ĺ�·�������г���A��ȥ��B�أ���֪AB���صľ���Ϊ40ǧ�ף��ұȼ�������1Сʱ��������;�о���Ϣ��0.5Сʱ���׳���2Сʱ��ʱ�ҵ��ٶ��Ǵ�ʱ���ٶȵ�1.2��������������A�صľ���y��ǧ�ף������ʻ��ʱ��t��Сʱ���ĺ�����ϵͼ����ͼ��ʾ������˵������ȷ�ĸ���Ϊ��������
����������ͬһ����ֱ�Ĺ�·�������г���A��ȥ��B�أ���֪AB���صľ���Ϊ40ǧ�ף��ұȼ�������1Сʱ��������;�о���Ϣ��0.5Сʱ���׳���2Сʱ��ʱ�ҵ��ٶ��Ǵ�ʱ���ٶȵ�1.2��������������A�صľ���y��ǧ�ף������ʻ��ʱ��t��Сʱ���ĺ�����ϵͼ����ͼ��ʾ������˵������ȷ�ĸ���Ϊ���������ټ���Ϣ֮ǰ���ٶ�Ϊ15ǧ��/Сʱ��
������Ϣ֮ǰ���ٶ�Ϊ20ǧ��/Сʱ��
�ۼ׳���2Сʱ��ʱ�������˵ľ���Ϊ
| 40 |
| 3 |
���ұȼ�����B��0.5Сʱ��
| A��1�� | B��2�� | C��3�� | D��4�� |
��ϰ��ϵ�д�
 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
�����Ŀ
��֪����y=��k-1��x+k-2��kΪ�����������y����x���������С����ôk��ȡֵ��Χ�ǣ�������
| A��k��1 | B��k��1 | C��k��2 | D��k��2 |
��ֱ��y=-x+3����ƽ��m����λ����ֱ��y=2x+4�Ľ����ڵڶ����ޣ���m��ȡֵ��Χ�ǣ�������
| A��m��1 | B��m��-5 | C��-5��m��1 | D��m��1 |
���ֱ��y=k1x+1��y=k2x-4�Ľ�����x���ϣ���ôk1��k2���ڣ�������
| A��4 | B��-4 | C��1��4 | D��1����-4�� |
����m•m3�Ľ���ǣ�������
| A��m2 | B��m3 | C��m4 | D��2m3 |
���������У���ȷ���ǣ�������
| A��2x+2y=2xy | ||
| B����x2y3��2=x4y5 | ||
C����xy��2��
| ||
| D��2xy-3yx=xy |

 �糿��С������ͨ��ѧУΨһ��һ��·��ֱ·����ѧ��;�з����������У�ͣ���������绰������ӵ��绰����Ϸ������ϸ���ѧУ��ͬʱС�շ��أ�����������С����������ѧУ������ؼң�15�������赽�ң��پ���3����С�յ���ѧУ��С��ʼ����100��/�ֵ��ٶȲ��У�С�պ�����ľ���y����λ���ף���С�մ���绰��IJ���ʱ��t����λ���֣�֮��ĺ�����ϵ��ͼ����������˵����
�糿��С������ͨ��ѧУΨһ��һ��·��ֱ·����ѧ��;�з����������У�ͣ���������绰������ӵ��绰����Ϸ������ϸ���ѧУ��ͬʱС�շ��أ�����������С����������ѧУ������ؼң�15�������赽�ң��پ���3����С�յ���ѧУ��С��ʼ����100��/�ֵ��ٶȲ��У�С�պ�����ľ���y����λ���ף���С�մ���绰��IJ���ʱ��t����λ���֣�֮��ĺ�����ϵ��ͼ����������˵����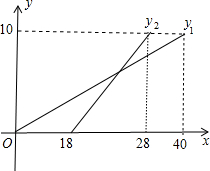 �ס�����������ͬ·��ǰ������ѧУ10km�ĿƼ����IJι�ѧϰ����ͼ��y1��y2�ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��y��km����ʱ��x���֣��仯�ĺ���ͼ������˵����
�ס�����������ͬ·��ǰ������ѧУ10km�ĿƼ����IJι�ѧϰ����ͼ��y1��y2�ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��y��km����ʱ��x���֣��仯�ĺ���ͼ������˵����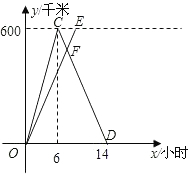 ��֪A��B�������600ǧ�ף��ס�������ͬʱ��A�dz���ʻ��B�ǣ��׳�����B�Ǻ�������ԭ·���أ���ͼ��������A�ǵľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ��������ʻ��7Сʱ�����������������н��ۣ�
��֪A��B�������600ǧ�ף��ס�������ͬʱ��A�dz���ʻ��B�ǣ��׳�����B�Ǻ�������ԭ·���أ���ͼ��������A�ǵľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ��������ʻ��7Сʱ�����������������н��ۣ�