题目内容
小明和小亮是某中学九年级的学生,他们参加了九年级上学期期末一中保送生选拔的考试,现只知道与甲、乙二人都进入了年段前4名.但该校保送生名额只有2名.试用画树形图或列表的方法求出:
(1)小明和小亮同时被保送的概率;
(2)小明和小亮至少有一人被保送的概率.
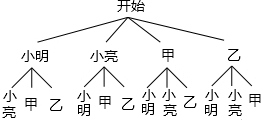 解:(1)画树状图得:
解:(1)画树状图得:∴一共有12种情况,
小明和小亮同时被保送的有2种情况,
∴小明和小亮同时被保送的概率为:
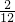 =
= ;
;(2)∵小明和小亮至少有一人被保送的有10种情况,
∴小明和小亮至少有一人被保送的概率为:
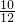 =
= .
.分析:(1)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;然后求得全部情况的总数与符合条件的情况数目,再求二者的比值即是其发生的概率;
(2)求得小明和小亮至少有一人被保送的数目,利用概率公式求解即可.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目