题目内容
如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF, 下列条件不能判定△ABC≌△DEF的是( )
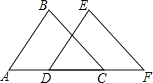
A. AD=CF B. ∠BCA=∠F C. ∠B=∠E D. BC=EF
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
题目内容
如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF, 下列条件不能判定△ABC≌△DEF的是( )

A. AD=CF B. ∠BCA=∠F C. ∠B=∠E D. BC=EF
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案