题目内容
已知⊙O的半径是6,弦AB的长为x2-5x-6=0的一个根,则圆心O到弦AB的距离以及AB所对的圆心角分别为
- A.
 和30°
和30° - B.
 和60°
和60° - C.3
 和30°
和30° - D.3
 和60°
和60°
D
分析:求出方程x2-5x-6=0的解,确定出弦AB的长,过O作OC⊥AB,连接OA,OB,如图所示,利用垂径定理得到C为AB的中点,由AB的长求出AC的长,在直角三角形AOC中,利用勾股定理求出OC的长,即为圆心O到弦AB的距离;由OA=OB=AB=6,得到三角形AOB为等边三角形,可得出∠AOB=60°,即为AB所对的圆心角的度数.
解答: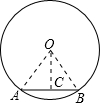 解:方程x2-5x-6=0因式分解得:(x-6)(x+1)=0,
解:方程x2-5x-6=0因式分解得:(x-6)(x+1)=0,
解得:x=6或x=-1(舍去),
∴AB=6,
过O作OC⊥AB,连接OA,OB,如图所示,
可得C为AB的中点,即AC=BC=3,
在Rt△AOC中,OA=6,AC=3,
根据勾股定理得:OC=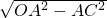 =3
=3 ,
,
∵OA=OB=AB=6,
∴△OAB为等边三角形,
∴∠AOB=60°,
则圆心O到弦AB的距离以及AB所对的圆心角分别为3 和60°.
和60°.
故选D
点评:此题考查了垂径定理,勾股定理,以及一元二次方程-因式分解法,利用了数形结合的思想,熟练掌握定理是解本题的关键.
分析:求出方程x2-5x-6=0的解,确定出弦AB的长,过O作OC⊥AB,连接OA,OB,如图所示,利用垂径定理得到C为AB的中点,由AB的长求出AC的长,在直角三角形AOC中,利用勾股定理求出OC的长,即为圆心O到弦AB的距离;由OA=OB=AB=6,得到三角形AOB为等边三角形,可得出∠AOB=60°,即为AB所对的圆心角的度数.
解答:
 解:方程x2-5x-6=0因式分解得:(x-6)(x+1)=0,
解:方程x2-5x-6=0因式分解得:(x-6)(x+1)=0,解得:x=6或x=-1(舍去),
∴AB=6,
过O作OC⊥AB,连接OA,OB,如图所示,
可得C为AB的中点,即AC=BC=3,
在Rt△AOC中,OA=6,AC=3,
根据勾股定理得:OC=
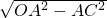 =3
=3 ,
,∵OA=OB=AB=6,
∴△OAB为等边三角形,
∴∠AOB=60°,
则圆心O到弦AB的距离以及AB所对的圆心角分别为3
 和60°.
和60°.故选D
点评:此题考查了垂径定理,勾股定理,以及一元二次方程-因式分解法,利用了数形结合的思想,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=( )
| A、4 | ||
B、4
| ||
C、4
| ||
D、2
|
已知圆的半径是1cm,弦AB所对的圆心角的度数120°,那么弦AB的长是多少cm( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|