题目内容
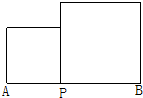 如图,AB=a,P是线段AB上一点,分别以AP、BP为边作正方形,设两个正方形的面积和用“S”来表示.
如图,AB=a,P是线段AB上一点,分别以AP、BP为边作正方形,设两个正方形的面积和用“S”来表示.(1)当AP=x时,写出S的表达式;
(2)当AP分别为
| 1 |
| 3 |
| 1 |
| 4 |
分析:(1)由AP=x,推出BP的长度,即可推出S的表达式,然后运用完全平方公式、合并同类项即可推出最后结果,(2)根据(1)解题思路,即可推出S关于a的表达式,然后,通过乘法运算,合并同类项即可推出最后结果,然后进行比较大小即可.
解答:解:(1)S=x2+(a-x)2
=x2+a2-2ax+x2
=2x2+a2-2ax
(2)当AP=
a时,S=(
a)2+(a-
a)2
=
a2
当AP=
a时,S=(
a)2+(a-
a)2
=
a2
又
a2<
a2
∴当AP为
a时S小于当AP为
a时.
=x2+a2-2ax+x2
=2x2+a2-2ax
(2)当AP=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 5 |
| 9 |
当AP=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 5 |
| 8 |
又
| 5 |
| 9 |
| 5 |
| 8 |
∴当AP为
| 1 |
| 3 |
| 1 |
| 4 |
点评:本题主要考查正方形的面积公式、整式的混合运算法则、完全平方公式,关键在于熟练掌握正方形的面积公式、熟练运用完全平方公式、认真合并同类项.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
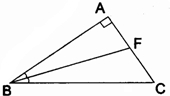 27、如图,AB⊥AC,BF是∠ABC的角平分线,若∠BFC=110°,求∠C的度数?
27、如图,AB⊥AC,BF是∠ABC的角平分线,若∠BFC=110°,求∠C的度数? 如图,AB∥CD,FG是∠EFC的平分线,并且∠1=50°,则∠2=
如图,AB∥CD,FG是∠EFC的平分线,并且∠1=50°,则∠2=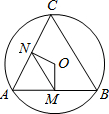 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果BC=6,那么MN=
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果BC=6,那么MN=