��Ŀ����
�˽̰�̿���Է�ʽ��������Ĺ������£������ʽ����ʱ��ȥ��ĸ��������ʽ���̵Ľ��п���ʹԭ��ʽ�����еķ�ĸΪ0�����Ӧ���¼��飺����ʽ���̵Ľ�������ĸ��������ĸ��ֵ��Ϊ0������ʽ���̵Ľ���ԭ��ʽ���̵Ľ⣻��������ⲻ��ԭ��ʽ���̵Ľ⣮��
������ݶ���λ������⣬����������⣺��֪����x�ķ��� �⣬����
�⣬���� ��һ������m��
��һ������m��
��1����m��k��ֵ��
��2���� ����һ������
����һ������
���𰸡�
�⣺��1����ʽ����ȥ��ĸ�ã�m��1��x=0��
�����⽫x=1����ã�m��1��1=0����m=2��
�൱m=2ʱ������x�ķ��� �⡣
�⡣
��m=2���뷽�̵ã�4+2k+6=0����k=��5��
��2���跽����һ��Ϊa������2a=6����a=3��
��� ����һ������3��
����һ������3��
��������
�����������1����ʽ����ȥ��ĸת��Ϊ��ʽ���̣��ɷ�ʽ�����⣬�ʽ�x=1������ʽ���̣��������m��ֵ����m��ֵ������֪���̼������k��ֵ��
��2�����ø���ϵ���Ĺ�ϵ����������̵���һ����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
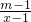 -
- =0�⣬����x2+kx+6=0��һ������m��
=0�⣬����x2+kx+6=0��һ������m�� -
- =0�⣬����x2+kx+6=0��һ������m��
=0�⣬����x2+kx+6=0��һ������m��