题目内容
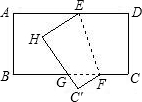 将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=
将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=
- A.55°
- B.65°
- C.72.5
- D.75°
C
分析:由折叠的性质知可以求出,折叠的性质是折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解题时要找到对应边和角.
解答:∠HEF=∠FED,
∵AE∥BC,HE∥C′F,
∴∠AEH=∠GFC′=90°-∠FGC′=90°-∠HGB=35°,
∴∠HEF=(180°-∠AEH)÷2=72.5°.
故选C.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
2、平行线的性质,直角三角形的性质,对顶角的概念求解.
分析:由折叠的性质知可以求出,折叠的性质是折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解题时要找到对应边和角.
解答:∠HEF=∠FED,
∵AE∥BC,HE∥C′F,
∴∠AEH=∠GFC′=90°-∠FGC′=90°-∠HGB=35°,
∴∠HEF=(180°-∠AEH)÷2=72.5°.
故选C.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
2、平行线的性质,直角三角形的性质,对顶角的概念求解.

练习册系列答案
相关题目
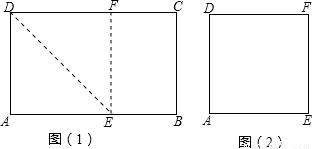
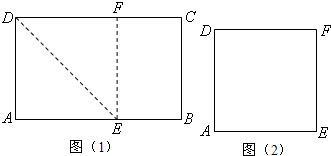 24、同学们在小学阶段做过这样的折纸游戏:把一个长方形纸片经过折叠可以得到新的四边形.如图(1),将长方形ABCD沿DE折叠,使点A与点F重合,再沿EF剪开,即得图(2)中的四边形DAEF.
24、同学们在小学阶段做过这样的折纸游戏:把一个长方形纸片经过折叠可以得到新的四边形.如图(1),将长方形ABCD沿DE折叠,使点A与点F重合,再沿EF剪开,即得图(2)中的四边形DAEF.
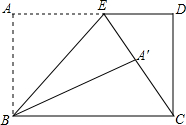 如图,长方形ABCD中,AB=15cm,点E在AD上且AE=9cm,连接EC,将长方形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处.求A′C的长.
如图,长方形ABCD中,AB=15cm,点E在AD上且AE=9cm,连接EC,将长方形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处.求A′C的长.