题目内容
求证：三角形两边的积等于其外接圆的直径与第三边的高的积．分析：连BE，利用AD是△ABC中BC边上的高，AE是⊙O直径，求证△ADC∽△ABE，利用相似三角形的对应边成比例即可求得．
解答：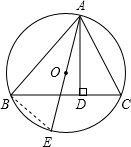
已知：⊙O是△ABC的外接圆，AD是△ABC中BC边上的高，AE是⊙O直径．
求证：AB•AC=AD•AE．
证明：连BE．AE是直径，∠ABE=90°，
AD⊥BC，∠ADC=90°，∠ABE=∠ADC，∠C=∠E，
△ADC∽△ABE，
=
，
即AB•AC=AD•AE．
．
已知：⊙O是△ABC的外接圆，AD是△ABC中BC边上的高，AE是⊙O直径．求证：AB•AC=AD•AE．
证明：连BE．AE是直径，∠ABE=90°，
AD⊥BC，∠ADC=90°，∠ABE=∠ADC，∠C=∠E，
△ADC∽△ABE，
| AC |
| AE |
| AD |
| AB |
即AB•AC=AD•AE．
．
点评：此题考查学生对相似三角形的判定与性质和三角形的外接圆与外心的理解和掌握，解答此题的关键是连解BE，利用相似三角形的对应边成比例很容易得出答案，但是如果没有作好辅助线，解答此题就有难度了，因此属于中档题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
求证：三角形两边的