Question

某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：

　　●操作发现：

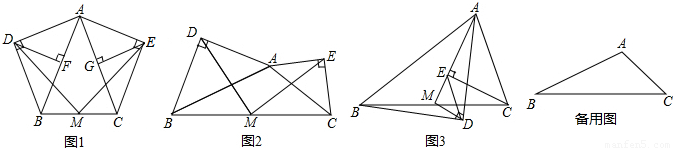
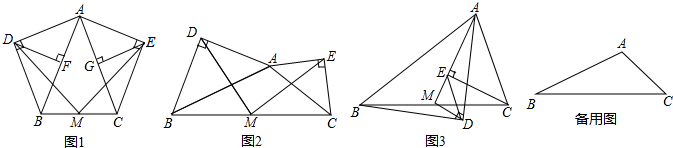
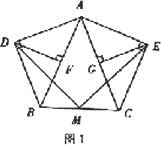
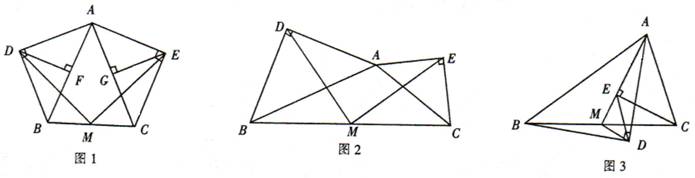
      在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是         （填序号即可）

     ①AF=AG=AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．

●数学思考：

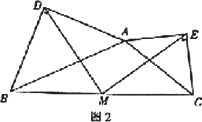
  在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程；

●类比探索：

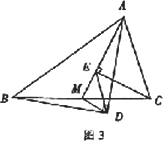
  在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．

  答：           ．

Answer 1

【答案】 解：

●操作发现：①②③④

●数学思考：

答：MD=ME，MD⊥ME，

１、MD=ME；

如图2，分别取AB，AC的中点F，G，连接DF，MF，MG，EG，

∵M是BC的中点，

∴MF∥AC，MF=AC．

又∵EG是等腰Rt△AEC斜边上的中线，

∴EG⊥AC且EG=AC，

∴MF=EG．

同理可证DF=MG．

∵MF∥AC，

∴∠MFA＋∠BAC=180°．

同理可得∠MGA+∠BAC=180°，

∴∠MFA=∠MGA．

又∵EG⊥AC，∴∠EGA=90°．

同理可得∠DFA=90°，

∴∠MFA+∠DFA=∠MGA=∠EGA，

即∠DFM=∠MEG，又MF=EG，DF=MG，

∴△DFM≌△MGE（SAS），

∴MD=ME．

2、MD⊥ME；

证法一：∵MG∥AB，

∴∠MFA+∠FMG=180°，

又∵△DFM≌△MGE，∴∠MEG=∠MDF.

∴∠MFA+∠FMD+∠DME+∠MDF=180°，

其中∠MFA+∠FMD+∠MDF=90°，

∴∠DME=90°.

即MD⊥ME；

证法二：如图2，MD与AB交于点H，

∵AB∥MG，

∴∠DHA=∠DMG，

又∵∠DHA=∠FDM+∠DFH,

即∠DHA=∠FDM+90°,

∵∠DMG=∠DME+∠GME，

∴∠DME=90°

即MD⊥ME；

●类比探究

答：等腰直角三解形

【考点解剖】  本题考查了轴对称、三角形中位线、平行四边形、直角三角形斜边上的中线等于斜边的一半、全等、角的转化等知识，能力要求很高．

【解题思路】  （1） 由图形的对称性易知①、②、③都正确，④∠DAB=∠DMB=45°也正确；（2）直觉告诉我们MD和ME是垂直且相等的关系，一般由全等证线段相等，受图1△DFM≌△MGE的启发，应想到取中点构造全等来证MD=ME，证MD⊥ME就是要证∠DME=90°，由△DFM≌△MGE得∠EMG=∠MDF, △DFM中四个角相加为180°，∠FMG可看成三个角的和，通过变形计算可得∠DME=90°． （3）只要结论，不要过程，在（2）的基础易知为等腰直角三解形.

【解答过程】  略.

【方法规律】  由特殊到一般，形变但本质不变（仍然全等）

【关键词】  课题学习  全等   开放探究