题目内容
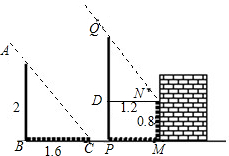
在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.

2.3m
试题分析:过N点作ND⊥PQ于D,则可得△ABC∽△QDN,根据相似三角形的对应边成比例可得QD的长,从而求得结果。
过N点作ND⊥PQ于D,
∴△ABC∽△QDN,
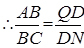
又∵AB=2,BC=1.6,PM=1.2,NM=0.8,
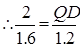 ,
,解得
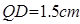 ,
,∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木竿PQ的长度为2.3米.
点评:解答本题的关键是把实际问题抽象到相似三角形中,利用相似三角形的对应边成比例,列出方程,通过解方程求出木竿PQ的长度.

练习册系列答案
相关题目
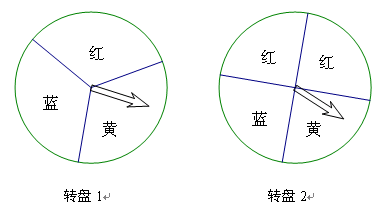
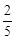 ,那么n等于 ( )
,那么n等于 ( )