题目内容
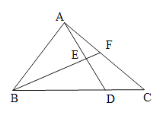
【题目】如图，△ABC的面积为40cm2，AE＝ED，BD＝3DC，则图中△AEF的面积等于______cm2.
【答案】
【解析】
连接DF，根据AE=ED，BD=3DC，可知S△AEF=S△EFD，S△ABE=S△BED，S△BDF=3S△FDC，S△ABD=3S△ADC，从而求得S△BDE＝15，设△AEF面积为x，根据△ABC的面积等于40cm2即可列方程x+x+ S△BDE + S△BDE +
（x+ S△BDE）=40，解方程即可．
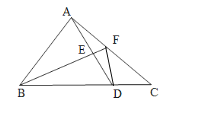
如图，连接DF，
∵AE=ED，BD=3DC，
∴S△AEF=S△EFD，S△ABE=S△BED，S△BDF=3S△FDC，S△ABD=3S△ADC,
又∵△ABC的面积为40cm2，
∴S△ABD=3S△ADC=30,
又∵AE＝ED，
∴S△BDE＝15，
设△AEF面积为x，
则x+x+ S△BDE + S△BDE +（x+ S△BDE）=40，
解得x＝．
故答案是：．
练习册系列答案
相关题目
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 | 学生数（名） | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息，解答下列问题：
（1）m= ， n= ， p=；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
