题目内容
已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为(-3| 3 |
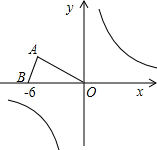 点B的坐标为(-6,0).
点B的坐标为(-6,0).(1)若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=
6
| ||
| x |
(3)若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数y=
| k |
| x |
分析:(1)若△OAB、△OA′B′关于y轴对称,那么A、A′以及B、B′都关于y轴对称,可据此得到A′、B′的坐标.
(2)由于点A向右平移过程中,点A的纵坐标没有变化,由此求得平移后的点A横坐标,然后同平移前的点A横坐标进行比较,即可得到平移的距离a的值.
(3)由于旋转前后,OB的长度没有发生变化,再结合旋转的角度即可求得旋转后的点B坐标,然后将其代入反比例函数的解析式中,即可求得k的值.
(2)由于点A向右平移过程中,点A的纵坐标没有变化,由此求得平移后的点A横坐标,然后同平移前的点A横坐标进行比较,即可得到平移的距离a的值.
(3)由于旋转前后,OB的长度没有发生变化,再结合旋转的角度即可求得旋转后的点B坐标,然后将其代入反比例函数的解析式中,即可求得k的值.
解答:解:(1)由于△OAB关于y轴的轴对称图形是△OA'B',所以A、A′关于y轴对称,B、B′关于y轴对称;
已知:点A的坐标为(-3
,3),点B的坐标为(-6,0),
故:A′(3
,3),B'(6,0).
(2)∵点A落在y=
上,设为A(x,y),
把y1=3代入,∴x1=2
;
∴a=x1-(-3
)=5
,
∴a=5
.
(3)B点坐标为(-6,0),
∵α=30°,此时A与B关于x轴对称,
∵点A的坐标为(-3
,3),
∴旋转后B点的坐标是(-3
,-3),
∴k=9
.
已知:点A的坐标为(-3
| 3 |
故:A′(3
| 3 |
(2)∵点A落在y=
6
| ||
| x |
把y1=3代入,∴x1=2
| 3 |
∴a=x1-(-3
| 3 |
| 3 |
∴a=5
| 3 |
(3)B点坐标为(-6,0),
∵α=30°,此时A与B关于x轴对称,
∵点A的坐标为(-3
| 3 |
∴旋转后B点的坐标是(-3
| 3 |
∴k=9
| 3 |
点评:此题考查了图形的几何变换、函数图象上点的坐标意义以及用待定系数法确定反比例函数解析式的方法,难度不大.

练习册系列答案
相关题目
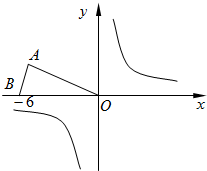 为(-6,0).
为(-6,0). 已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(
已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(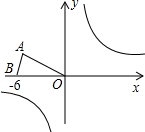 已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(
已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为( ),点B的坐标为(-6,0).
),点B的坐标为(-6,0). 的图象上,求a的值;
的图象上,求a的值; 的图象上,求k的值;
的图象上,求k的值;