题目内容
(2007•柳州)如图所示,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与x轴交于A、B两点(A在B的左侧),与y轴交于C点.(1)试判断b与c的积是正数还是负数,为什么?
(2)如果AB=4,且当抛物线y=-x2+bx+c的图象向左平移一个单位时,其顶点在y轴上.
①求原抛物线的表达式;
②设P是线段OB上的一个动点,过点P作PE⊥x轴交原抛物线于E点.问:是否存在P点,使直线BC把△PCE分成面积之比为3:1的两部分?若存在,求出P点的坐标;若不存在,请说明理由.
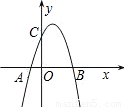
【答案】分析:(1)由图象可知:抛物线与y轴交点在y轴正半轴,因此c>0,抛物线对称轴在y轴右侧,那么对称轴方程也大于0据此可求出b的符号,进而可求出b、c积的符号.
(2)①抛物线对称轴向左平移一个单位时,抛物线对称轴为y轴,则说明原抛物线的对称轴为x=1,可根据AB=4,求出A、B的坐标,然后代入抛物线的解析式中,即可求出原抛物线的解析式.
②如果设PE与BC的交点为F的话,那么EF长就是两函数差的绝对值,而PF的长就是直线BC的函数值.那么根据等高三角形的面积比等于底边比,可得出当直线BC分三角形PCE的面积为3:1两部分时,有两种情况:
(I)EF:PF=3:1;
(II)EF:PF=1:3;然后将上面所说的EF,PF的表达式代入不同的比例关系式中,即可求出P点的坐标.
解答:解:(1)由图象知:c>0,且x=-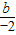 >0,即b>0,
>0,即b>0,
因此bc>0,
(2)由题意知:原抛物线的对称轴为x=1,
∵AB=4,
∴A(-1,0),B(3,0),
已知A、B均在原抛物线上,则有:
 ,
,
解得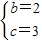 ,
,
∴原抛物线的解析式为y=-x2+2x+3.

②如图:设直线BC与PE的交点为F,
由于△CEF和△CPF等高,因此面积比等于EF和PF的比.
易知:直线BC的解析式为:y=-x+3,
设P点坐标为(m,0),(m>0)则有E(m,-m2+2m+3),F(m,-m+3),
∴EF=-m2+2m+3-(-m+3)=-m2+3m=m(-m+3),PF=-m+3,
①当EF:PF=3:1时,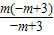 =
= ,解得m=3,经检验m=3是增根,不合题意舍去;
,解得m=3,经检验m=3是增根,不合题意舍去;
②当EF:PF=1:3时,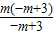 =
= ,解得m=
,解得m= ,经检验m=
,经检验m= 是原方程的解.
是原方程的解.
∴存在符合条件的P点,且坐标为P( ,0).
,0).
点评:本题考查了二次函数解析式的确定、图形面积的求法等知识,要注意的是(2)(II)中在不确定直线BC分三角形PCE的两部分谁大谁小的情况下要分类讨论,不要漏解.
(2)①抛物线对称轴向左平移一个单位时,抛物线对称轴为y轴,则说明原抛物线的对称轴为x=1,可根据AB=4,求出A、B的坐标,然后代入抛物线的解析式中,即可求出原抛物线的解析式.
②如果设PE与BC的交点为F的话,那么EF长就是两函数差的绝对值,而PF的长就是直线BC的函数值.那么根据等高三角形的面积比等于底边比,可得出当直线BC分三角形PCE的面积为3:1两部分时,有两种情况:
(I)EF:PF=3:1;
(II)EF:PF=1:3;然后将上面所说的EF,PF的表达式代入不同的比例关系式中,即可求出P点的坐标.
解答:解:(1)由图象知:c>0,且x=-
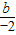 >0,即b>0,
>0,即b>0,因此bc>0,
(2)由题意知:原抛物线的对称轴为x=1,
∵AB=4,
∴A(-1,0),B(3,0),
已知A、B均在原抛物线上,则有:
 ,
,解得
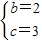 ,
,∴原抛物线的解析式为y=-x2+2x+3.

②如图:设直线BC与PE的交点为F,
由于△CEF和△CPF等高,因此面积比等于EF和PF的比.
易知:直线BC的解析式为:y=-x+3,
设P点坐标为(m,0),(m>0)则有E(m,-m2+2m+3),F(m,-m+3),
∴EF=-m2+2m+3-(-m+3)=-m2+3m=m(-m+3),PF=-m+3,
①当EF:PF=3:1时,
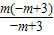 =
= ,解得m=3,经检验m=3是增根,不合题意舍去;
,解得m=3,经检验m=3是增根,不合题意舍去;②当EF:PF=1:3时,
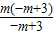 =
= ,解得m=
,解得m= ,经检验m=
,经检验m= 是原方程的解.
是原方程的解.∴存在符合条件的P点,且坐标为P(
 ,0).
,0).点评:本题考查了二次函数解析式的确定、图形面积的求法等知识,要注意的是(2)(II)中在不确定直线BC分三角形PCE的两部分谁大谁小的情况下要分类讨论,不要漏解.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目