题目内容
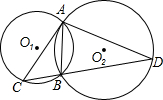
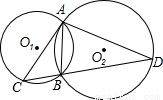
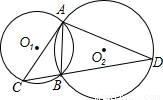
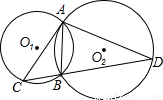
如图，已知⊙Ol与⊙O2相交于A、B两点，过点A作⊙Ol的弦AC，连接CB并延长交⊙O2于点D，连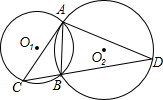
AD．若∠CAB=∠D．（1）求证：AC是⊙O2的切线；
（2）若AB：AD=1：2，CD=6，求AC的长．
分析：（1）连A02并延长交⊙O2于E，连BE，易得Rt△ABE，根据角相等的关系转化可得∠CAE=90°，即AC⊥AO2故AC是⊙O2的切线．
（2）易得△ACB∽△DCA，可得比例关系，代入数据AB：AD=1：2，CD=6，可得答案．
（2）易得△ACB∽△DCA，可得比例关系，代入数据AB：AD=1：2，CD=6，可得答案．
解答：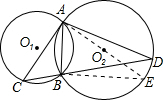
（1）证明：连A02并延长交⊙O2于E，连BE，（1分）
∵∠ABE=90°，
∴∠BAE+∠AEB=90°．
∵∠CAB=∠D，
∴∠BAE+∠CAB=90°．
∴∠CAE=90°，即AC⊥AO2．
故AC是⊙O2的切线．
（2）解：△ACB与△DCA中，
∵∠C=∠C，∠CAB=∠D，
∴△ACB∽△DCA．
∴AC=
×CD=3．
（1）证明：连A02并延长交⊙O2于E，连BE，（1分）∵∠ABE=90°，
∴∠BAE+∠AEB=90°．
∵∠CAB=∠D，
∴∠BAE+∠CAB=90°．
∴∠CAE=90°，即AC⊥AO2．
故AC是⊙O2的切线．
（2）解：△ACB与△DCA中，
∵∠C=∠C，∠CAB=∠D，
∴△ACB∽△DCA．
∴AC=
| AB |
| AD |
点评：本题考查常见的几何题型，包括切线的判定、线段长度的求法，要求学生掌握常见的解题方法，并能结合图形选择简单的方法解题．
练习册系列答案
相关题目
