题目内容
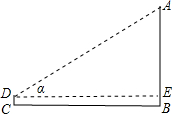
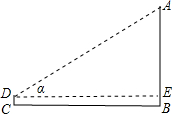如图，在与旗杆AB相距20米的C处，用1.2米的测角仪CD测得旗杆顶端的仰角α=30°，求旗杆AB的高（精确到0.1米）．
分析：根据题意：过点D作DE⊥AB，交AB与E；可得Rt△ADE，解之可得AE的大小；进而根据AB=BE+AE可得旗杆AB的高．
解答：解：过点D作DE⊥AB，交AB与E，
在Rt△ADE中，有α=30°，DE=20，
易得AE=DE×tan30°=
，
故AB=BE+AE=
+1.2≈11.5+1.2=12.7米．
在Rt△ADE中，有α=30°，DE=20，
易得AE=DE×tan30°=
20
| ||
| 3 |
故AB=BE+AE=
20
| ||
| 3 |
点评：本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
