题目内容
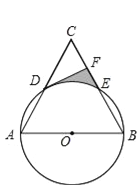
【题目】如图,AB是⊙O的一条弦,且AB=![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.

【答案】(1)OA=4;(2)∠BAF的度数是75°或15°.
【解析】
试题分析:(1)根据垂径定理求出AD的长,根据圆周角定理求出∠AOD的度数,运用正弦的定义解答即可;
(2)作OH⊥AF于H,根据勾股定理和等腰直角三角形的性质求出∠OAF的度数,分情况计算即可.
试题解析:(1)∵OC⊥AB,AB=![]() ,∴AD=DB=
,∴AD=DB=![]() ,∵∠E=30°,
,∵∠E=30°,
∴∠AOD=60°,∠OAB=30°,∴OA=4;
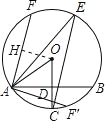
(2)如图,作OH⊥AF于H,∵OA=4,OH=![]() ,∴∠OAF=45°,
,∴∠OAF=45°,
∴∠BAF=∠OAF+∠OAB=75°,
则∠BAF′=∠OAF′﹣∠OAB=15°,
∴∠BAF的度数是75°或15°.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目