题目内容
已知在△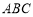 中,
中,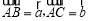 ,
,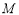 是边
是边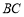 上的一点,
上的一点,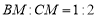 ,用向量
,用向量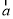 、
、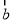 表示
表示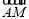 = .
= .
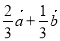
【解析】
试题分析:【解析】
∵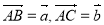 ,
,
∴ ,
,
∵BM:CM=1:2,
∴ ,
,
∴ =
=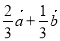 .
.
故答案为: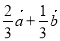 .
.
考点:平面向量.

练习册系列答案
相关题目
题目内容
已知在△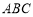 中,
中,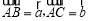 ,
,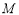 是边
是边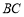 上的一点,
上的一点,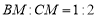 ,用向量
,用向量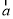 、
、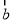 表示
表示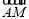 = .
= .
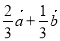
【解析】
试题分析:【解析】
∵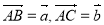 ,
,
∴ ,
,
∵BM:CM=1:2,
∴ ,
,
∴ =
=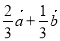 .
.
故答案为: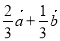 .
.
考点:平面向量.
