Question

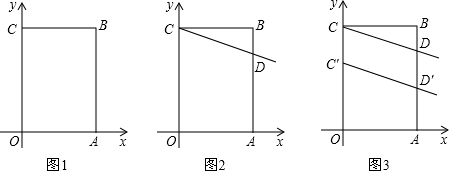
已知长方形OABC的长AB=5，宽BC=3，将它的顶点O落在平面直角坐标系的原点上，顶点A，C两点分别落在x，y轴上，点B在第一象限内，根据下列图示回答问题：
（1）如图1，写出点的坐标：A（

3，0

），B（

3，5

），C（

0，5

）；
（2）如图2，若过点C的直线CD交AB于D，且把长方形OABC的周长分为3：1两部分，则点D的坐标是（

3，4

）
（3）如图3，将（2）中的线段CD向下平移2个单位，得到C′D′，试计算四边形OAD′C′的面积．

Answer 1

分析：（1）根据平面直角坐标系的特点结合长方形的性质写出点A、B、C的坐标即可；
（2）根据长方形的周长公式求出长方形的周长，再根据比例求出OC+OA+AD的和，然后求出AD的长度，从而得解；
（3）求出OC′与AD′的长度，然后根据梯形的面积公式列式计算即可得解．

解答：解：（1）∵长方形OABC的长AB=5，宽BC=3，
∴点A、B、C的坐标分别为A（3，0），B（3，5），C（0，5）；

（2）长方形OABC的周长=2（5+3）=16，
∵长方形OABC的周长分为3：1两部分，
∴OC+OA+AD=

3

3+1

×16=12，
即5+3+AD=12，
解得AD=4，
∴点D的坐标为（3，4）；

（3）线段CD向下平移2个单位，
则OC′=5-2=3，AD′=4-2=2，
所以，四边形OAD′C′的面积=

1

2

（2+3）×3=

15

2

．
故答案为：（1）A（3，0），B（3，5），C（0，5）；（2）D（3，4）．

点评：本题考查了坐标与图形的性质，主要利用了矩形的性质，平面直角坐标系的特点，平移变换，理清点的动态变化过程是解题的关键．