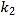题目内容
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足当m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
(2)若一次函数y=kx+b(k≠0)是闭间[m,n]上的“闭函数”,求此函数的解析式.
【答案】(1)是,理由见解析;(2)当k>0时,函数的解析式为y=x;当k<0时,函数的解析式为y=﹣x+m+n.
【解析】
(1)根据“闭函数”的定义验证反比例函数y=![]() 的函数值y是否满足1≤y≤2019即可;
的函数值y是否满足1≤y≤2019即可;
(2)分两种情况:当![]() 时和当
时和当![]() 时,分别用待定系数法求一次函数的解析式即可.
时,分别用待定系数法求一次函数的解析式即可.
(1)反比例函数y=![]() 是闭区间[1,2019]上的“闭函数”,
是闭区间[1,2019]上的“闭函数”,
理由:∵当x=1时,y=2019,当x=2019时,y=1,
∴反比例函数y=![]() 是闭区间[1,2019]上的“闭函数”;
是闭区间[1,2019]上的“闭函数”;
(2)∵一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
∴当k>0时,根据题意有
![]() 解得
解得![]() ,
,
即此函数的解析式为y=x;
当k<0时,根据题意有
![]() 解得
解得![]() ,
,
即此函数的解析式为y=﹣x+m+n.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目