题目内容
某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
解:(1)∵一等奖有一个,∴购买一等奖奖品的金额为x;
∵二等奖有4人,∴购买二等奖奖品的金额为4(x-15);
∵三等奖有5人,∴购买三等奖奖品的金额为5(x-30);
∴购买奖品总金额为y=x+4(x-15)+5(x-30),
即y=10x-210;
(2)∵500≤y≤600,
∴500≤10x-210≤600,即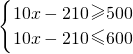 ,
,
解得:71≤x≤81,
由表可知,符合条件的有排球和篮球,
∴购买一等奖奖品的单价是74元(排球)或79元(篮球),
∴当一等奖买排球时,二等奖的价格为74-15=59元,三等奖品的价格为74-30=44元;
当一等奖买篮球时,二等奖的价格为79-15=64元,三等奖品的价格为79-30=49元;
∴有两种方案:
方案一:一等奖奖品买排球,二等奖奖品买旱冰鞋,三等奖奖品买围棋;
方案二:一等奖奖品买篮球,二等奖奖品买乒乓球,三等奖奖品买象棋;
本着尽可能节约资金的原则,应选择方案一:当x=74时,y=10x-210=10×74-210=530(元)结论:所需总金额为530元.
分析:(1)总金额为:y=一等奖奖品总价+二等奖奖品总价+三等奖奖品总价,需找到相应的单价和数量;
(2)根据500≤y≤600列出不等式组,求出x的取值范围,由表中所列出的奖品单价中找出符合x的取值范围的奖品,再根据各种奖品价格之间的关系求出另外两种奖品即可.
点评:读懂题意,找到相应的等量关系是解决本题的关键.会根据范围选取合适的物品.
∵二等奖有4人,∴购买二等奖奖品的金额为4(x-15);
∵三等奖有5人,∴购买三等奖奖品的金额为5(x-30);
∴购买奖品总金额为y=x+4(x-15)+5(x-30),
即y=10x-210;
(2)∵500≤y≤600,
∴500≤10x-210≤600,即
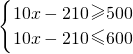 ,
,解得:71≤x≤81,
由表可知,符合条件的有排球和篮球,
∴购买一等奖奖品的单价是74元(排球)或79元(篮球),
∴当一等奖买排球时,二等奖的价格为74-15=59元,三等奖品的价格为74-30=44元;
当一等奖买篮球时,二等奖的价格为79-15=64元,三等奖品的价格为79-30=49元;
∴有两种方案:
方案一:一等奖奖品买排球,二等奖奖品买旱冰鞋,三等奖奖品买围棋;
方案二:一等奖奖品买篮球,二等奖奖品买乒乓球,三等奖奖品买象棋;
本着尽可能节约资金的原则,应选择方案一:当x=74时,y=10x-210=10×74-210=530(元)结论:所需总金额为530元.
分析:(1)总金额为:y=一等奖奖品总价+二等奖奖品总价+三等奖奖品总价,需找到相应的单价和数量;
(2)根据500≤y≤600列出不等式组,求出x的取值范围,由表中所列出的奖品单价中找出符合x的取值范围的奖品,再根据各种奖品价格之间的关系求出另外两种奖品即可.
点评:读懂题意,找到相应的等量关系是解决本题的关键.会根据范围选取合适的物品.

练习册系列答案
相关题目
某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
某单位团支部组织青年团员参加登山比赛。比赛奖次及所设人数为:一等奖1人,二等奖4人,三等奖5人,团支部要求一等奖奖品单价比二等奖奖品单价高l5元,二等奖奖品单价比三等奖奖品单价高l5元。设一等奖奖品的单价为![]() (元),团支部购买奖品总金额为
(元),团支部购买奖品总金额为![]() (元)。(1)求
(元)。(1)求![]() 与
与![]() 的函数关系式。(即函数表达式)
的函数关系式。(即函数表达式)
(2)因为团支部活动经费有限,购买奖品总金额应限制在:![]() ,在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案?然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
,在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案?然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运行衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |