Question

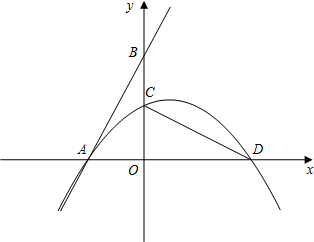
（2012•宁德质检）如图，在平面直角坐标系中，直线y=2x+2交x轴于点A，交y轴于点B，将△AOB绕原点O顺时针旋转90°后得到△COD，抛物线l经过点A、C、D．
（1）求点A、B的坐标；
（2）求抛物线l的解析式；
（3）已知在抛物线l与线段AD所围成的封闭图形（不含边界）中，存在点P（a，b），使得△PCD是等腰三角形，求a的取值范围．

Answer 1

分析：（1）根据直线y=2x+2交x轴于点A，交y轴于点B，分别令x=0，求出y的值，令y=0，求出x值，于是A、B两点的坐标可求出；
（2）设抛物线x的解析式是y=ax²+bx+c（a≠0），由旋转可知：OC=OA=1，OD=OB=2，把A（-1，0），C（0，1），D（2，0）代入解析式，求出a、b、c的值，抛物线的解析式即可求出；
（3）首先根据勾股定理求出CD的长度，若△PCD是等腰三角形，则有以下三种情况：①当CP=CD时，②当DP=DC时，③当PC=PD时，分别求出a的取值范围即可．

解答：解：（1）当x=0时，y=2；
当y=0时，由2x+2=0得x=-1．
∴A（-1，0），B（0，2）；

（2）由旋转可知：OC=OA=1，OD=OB=2，
∴C（0，1），D（2，0）．
设抛物线x的解析式是y=ax²+bx+c（a≠0）．
依题意，得

a-b+c=0 c=1 4a+2b+c=0

，
解得

a=- 1 2 b= 1 2 c=1

，
∴抛物线l的解析式是y=-

1

2

x²+

1

2

x+1；

（3）在Rt△COD中，由C（0，1），D（2，0）可得CD=

22+12

=

5

，
若△PCD是等腰三角形，则有以下三种情况：
①当CP=CD时，此时点P在抛物线l与线段AD所围成的封闭图形外，不合题意；
②当DP=DC时，以点D为圆心，DC长为半径画弧交x轴于点H，此时点P在

CH

上（不含点C、H），
此时a的取值范围是-

5

+2＜a＜0；          
③当PC=PD时，作线段CD的垂直平分线FG，交CD于点E，交x轴于点F，交抛物线于点G．
此时点P在线段FG上（不含点F、G、E），
求得 E（1，

1

2

），DE=

5

2

．
在Rt△DEF，Rt△DOC中，cos∠CDO=

DE

DF

=

DO

DC

，
∴

5 2

DF

=

2

5

，解得DF=

5

4

，
∴OF=2-

5

4

=

3

4

，即F（

3

4

，0）．
易得过E、F的直线解析式是y=2x-

3

2

，联立方程组得

y=2x- 3 2 y=- 1 2 x2+ 1 2 x+1

，
解得x₁=

-3+ 29

2

，x₂=

-3- 29

2

（舍去），
∴点G的横坐标是

-3+ 29

2

，
此时a的取值范围是

3

4

＜a＜

-3+ 29

2

，且a≠1．
综合①②③，当△PCD是等腰三角形时，a的取值范围是-

5

+2＜a＜0或

3

4

＜a＜

-3+ 29

2

，且a≠1．

点评：本题主要考查二次函数的综合题，此题设计直线与抛物线的交点问题，解答（3）问时需要进行分类讨论，此问同学们容易出现讨论不全的情况，此题难度较大．