题目内容
将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB=AC=8cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积约是| 3 |
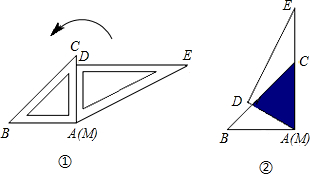
分析:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,根据AC=8,就可求出GF的长,从而求解.
解答: 解:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,设FC=x,则GF=FC=x,
解:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,设FC=x,则GF=FC=x,
∵旋转角为60°,即可得∠FAG=60°,
∴AF=GFcot∠FAG=
x.
所以x+
x=8,则x=12-4
.
所以S△AGC=
×8×(12-4
)≈20.3cm2.
故答案为:20.3.
 解:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,设FC=x,则GF=FC=x,
解:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,设FC=x,则GF=FC=x,∵旋转角为60°,即可得∠FAG=60°,
∴AF=GFcot∠FAG=
| ||
| 3 |
所以x+
| ||
| 3 |
| 3 |
所以S△AGC=
| 1 |
| 2 |
| 3 |
故答案为:20.3.
点评:本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 将一副三角板按如图的方式摆放在一起,连接AD,求∠ADB的正弦值?
将一副三角板按如图的方式摆放在一起,连接AD,求∠ADB的正弦值? 13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是
13、将一副三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是 10、如图,将一副三角板按如图放置,则下列结论
10、如图,将一副三角板按如图放置,则下列结论 如图,将一副三角板按如图所示叠放.
如图,将一副三角板按如图所示叠放. 将一副三角板按如图方式摆放,则图中不存在的角度是( )
将一副三角板按如图方式摆放,则图中不存在的角度是( )