题目内容
已知a与2b互为相反数,c与d互为倒数,x的绝对值等于3,则3cd-2(2a+4b)+
=
| x | 3 |
4或2
4或2
.分析:根据互为相反数的定义可得a+2b=0,互为倒数的定义可得cd=1,绝对值的性质求出x的值,然后代入代数式进行计算即可得解.
解答:解:∵a与2b互为相反数,
∴a+2b=0,
∵c与d互为倒数,
∴cd=1,
∵x的绝对值等于3,
∴x=3或-3,
∴3cd-2(2a+4b)+
=3cd-4(a+2b)+
=3-0+
=3+
,
当x=3时,原式=3+
=4,
当x=-3时,原式=3+
=2,
所以,代数式的值为4或2.
故答案为:4或2.
∴a+2b=0,
∵c与d互为倒数,
∴cd=1,
∵x的绝对值等于3,
∴x=3或-3,
∴3cd-2(2a+4b)+
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
当x=3时,原式=3+
| 3 |
| 3 |
当x=-3时,原式=3+
| -3 |
| 3 |
所以,代数式的值为4或2.
故答案为:4或2.
点评:本题考查了代数式求值,主要利用了相反数的定义,倒数的定义,以及绝对值的性质,是基础题,需要注意x的值有两个.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
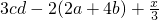 =________.
=________. 互为相反数,|x|=4,求4ab-2c+d+
互为相反数,|x|=4,求4ab-2c+d+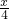 的值.
的值.