题目内容
如图是利用四边形的不稳定性制作的菱形衣帽架.已知其中每个菱形的边长都为20cm,且∠1=60°,在A、B、C各处都钉一个铁钉把衣帽架钉在墙壁上,则B、C两个铁钉之间的距离为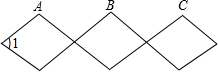
分析:连接BC,求证四边形BEDC为平行四边形,得BC=DE,进而求证△BEF为等边三角形,得BF=BE,根据菱形对角线垂直的性质得Rt△BEG,根据BE、BG的长可以求得EG,根据EG即可求DE,即BC的长度.
解答:解:连接BC,如下图
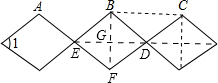
∵BE=CD,BE∥CF
∴四边形BEDC为平行四边形,
∴BC=DE,
∵∠1=60°,即∠BEF=60°,BE=EF
∴△BEF为等边三角形,即BF=BE=20cm,BG=10cm,
∴在Rt△BEG中,BE=20cm,BG=10cm,
∴EG=
=10
cm,
∴BC=DE=2EG=20
cm,
故答案为 20
.

∵BE=CD,BE∥CF
∴四边形BEDC为平行四边形,
∴BC=DE,
∵∠1=60°,即∠BEF=60°,BE=EF
∴△BEF为等边三角形,即BF=BE=20cm,BG=10cm,
∴在Rt△BEG中,BE=20cm,BG=10cm,
∴EG=
| BE2-BG2 |
| 3 |
∴BC=DE=2EG=20
| 3 |
故答案为 20
| 3 |
点评:本题考查了平行四边形的判定,考查了菱形各边长相等、对角线垂直平分的性质,考查了勾股定理在直角三角形中的运用,本题中运用勾股定理求EG是解题的关键.

练习册系列答案
相关题目
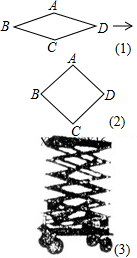 (2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.


 ≈1.41]
≈1.41]  ≈1.41].
≈1.41].
 ≈1.41].
≈1.41].