题目内容
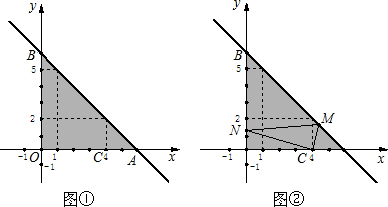
如图①,过点(1,5)和(4,2)两点的直线分别与x轴、y轴交于A、B两点.(1)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.图中阴影部分(不包括边界)所含格点的个数有
(2)设点C(4,0),点C关于直线AB的对称点为D,请直接写出点D的坐标
(3)如图②,请在直线AB和y轴上分别找一点M、N使△CMN的周长最短,在图②中作出图形,并求出点N的坐标.
分析:(1)先利用待定系数法求得直线AB的解析式为y=-x+6;再分别把x=2、3、4、5代入,求出对应的纵坐标,从而得到图中阴影部分(不包括边界)所含格点的坐标;
(2)首先根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D的坐标;
(3)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.由D、E两点的坐标利用待定系数法求出直线DE的解析式,再根据y轴上点的坐标特征,即可求出点N的坐标.
(2)首先根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D的坐标;
(3)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.由D、E两点的坐标利用待定系数法求出直线DE的解析式,再根据y轴上点的坐标特征,即可求出点N的坐标.
解答: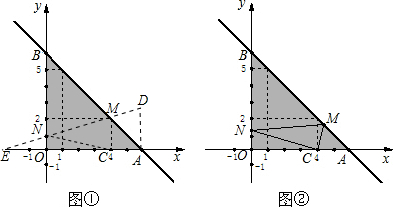 解:(1)设直线AB的解析式为y=kx+b,
解:(1)设直线AB的解析式为y=kx+b,
把(1,5),(4,2)代入得,
kx+b=5,4k+b=2,
解得k=-1,b=6,
∴直线AB的解析式为y=-x+6;
当x=2,y=4;
当x=3,y=3;
当x=4,y=2;
当x=5,y=1.
∴图中阴影部分(不包括边界)所含格点的有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),
(3,1),(3,2),
(4,1).
一共10个;
(2)∵直线y=-x+6与x轴、y轴交于A、B两点,
∴A点坐标为(6,0),B点坐标为(0,6),
∴OA=OB=6,∠OAB=45°.
∵点C关于直线AB的对称点为D,点C(4,0),
∴AD=AC=2,AB⊥CD,
∴∠DAB=∠CAB=45°,
∴∠DAC=90°,
∴点D的坐标为(6,2);
(3)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则NC=NE,点E(-4,0).
又∵点C关于直线AB的对称点为D,∴CM=DM,
∴△CMN的周长=CM+MN+NC=DM+MN+NE=DE,此时周长最短.
设直线DE的解析式为y=mx+n.
把D(6,2),E(-4,0)代入,得
6m+n=2,-4m+n=0,
解得m=
,n=
,
∴直线DE的解析式为y=
x+
.
令x=0,得y=
,
∴点N的坐标为(0,
).
故答案为10;(6,2).
 解:(1)设直线AB的解析式为y=kx+b,
解:(1)设直线AB的解析式为y=kx+b,把(1,5),(4,2)代入得,
kx+b=5,4k+b=2,
解得k=-1,b=6,
∴直线AB的解析式为y=-x+6;
当x=2,y=4;
当x=3,y=3;
当x=4,y=2;
当x=5,y=1.
∴图中阴影部分(不包括边界)所含格点的有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),
(3,1),(3,2),
(4,1).
一共10个;
(2)∵直线y=-x+6与x轴、y轴交于A、B两点,
∴A点坐标为(6,0),B点坐标为(0,6),
∴OA=OB=6,∠OAB=45°.
∵点C关于直线AB的对称点为D,点C(4,0),
∴AD=AC=2,AB⊥CD,
∴∠DAB=∠CAB=45°,
∴∠DAC=90°,
∴点D的坐标为(6,2);
(3)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则NC=NE,点E(-4,0).
又∵点C关于直线AB的对称点为D,∴CM=DM,
∴△CMN的周长=CM+MN+NC=DM+MN+NE=DE,此时周长最短.
设直线DE的解析式为y=mx+n.
把D(6,2),E(-4,0)代入,得
6m+n=2,-4m+n=0,
解得m=
| 1 |
| 5 |
| 4 |
| 5 |
∴直线DE的解析式为y=
| 1 |
| 5 |
| 4 |
| 5 |
令x=0,得y=
| 4 |
| 5 |
∴点N的坐标为(0,
| 4 |
| 5 |
故答案为10;(6,2).
点评:本题考查了待定系数法求一次函数的解析式,横纵坐标都为整数的点的坐标的确定方法,轴对称的性质及轴对称-最短路线问题,综合性较强,有一定难度.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
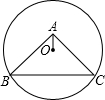 如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )A、
| ||
B、2
| ||
C、3
| ||
D、
|
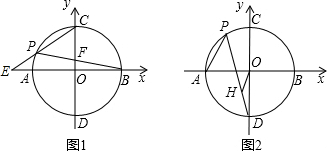
 如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
 已知:如图A,△ABC各角的平分线AD,BE,CF交于点O.
已知:如图A,△ABC各角的平分线AD,BE,CF交于点O.