��Ŀ����
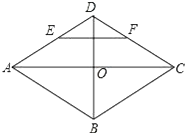
����Ŀ����ͼ������OABC���������������ϣ���A������Ϊ��10��0����������![]() ����B��C���㣬����x���һ������ΪD����2��0������P���߶�CB�ϵĶ��㣬��CP=t��0��t��10����
����B��C���㣬����x���һ������ΪD����2��0������P���߶�CB�ϵĶ��㣬��CP=t��0��t��10����
��1����ֱ��д��B��C��������꼰�����ߵĽ���ʽ��
��2������P��PE��BC�����������ڵ�E������BE����tΪ��ֵʱ����PBE=��OCD��
��3����Q��x���ϵĶ��㣬����P��PM��BQ����CQ�ڵ�M����PN��CQ����BQ�ڵ�N�����ı���PMQNΪ������ʱ�������t��ֵ��
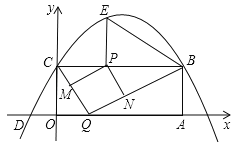
���𰸡���1��B��10��4����C��0��4����![]() ����2��3����3��t��ֵΪ
����2��3����3��t��ֵΪ![]() ��
��![]() ��
��
��������
�����������1���������ߵĽ���ʽ�����C�����꣬�ɾ��ε����ʿ����B�����꣬��B��D�����꣬���ô���ϵ��������������߽���ʽ��
��2������P��t��4������ɱ�ʾ��E�����꣬�Ӷ��ɱ�ʾ��PB��PE�ij�����������֤����PBE�ס�OCD���������������ε����ʿɵõ�����t�ķ��̣������t��ֵ��
��3�����ı���PMQNΪ������ʱ�����֤����COQ�ס�QAB���������������ε����ʿ����CQ�ij�����Rt��BCQ�п����BQ��CQ�������t�ֱ��ʾ��PM��PN���ɵõ�����t�ķ��̣������t��ֵ��
���������
��1����![]() �У���x=0�ɵ�y=4����C��0��4�������ı���OABCΪ���Σ���A��10��0������B��10��4������B��D������������߽���ʽ�ɵ���
�У���x=0�ɵ�y=4����C��0��4�������ı���OABCΪ���Σ���A��10��0������B��10��4������B��D������������߽���ʽ�ɵ���![]() �������
�������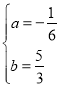 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2�����������P��t��4������E��t��![]() ������PB=10��t��PE=
������PB=10��t��PE=![]() ��4=
��4=![]() ���ߡ�BPE=��COD=90�㣬��PBE=��OCD�����PBE�ס�OCD����
���ߡ�BPE=��COD=90�㣬��PBE=��OCD�����PBE�ס�OCD����![]() ����BPOD=COPE����2��10��t��=4��
����BPOD=COPE����2��10��t��=4��![]() �������t=3��t=10���������⣬��ȥ��������t=3ʱ����PBE=��OCD��
�������t=3��t=10���������⣬��ȥ��������t=3ʱ����PBE=��OCD��
��3�����ı���PMQNΪ������ʱ������PMC=��PNB=��CQB=90�㣬PM=PN�����CQO+��AQB=90�㣬�ߡ�CQO+��OCQ=90�㣬���OCQ=��AQB����Rt��COQ��Rt��QAB����![]() ����OQAQ=COAB����OQ=m����AQ=10��m����m��10��m��=4��4�����m=2��m=8��
����OQAQ=COAB����OQ=m����AQ=10��m����m��10��m��=4��4�����m=2��m=8��
����m=2ʱ��CQ=![]() =
=![]() ��BQ=
��BQ=![]() =
=![]() ����sin��BCQ=
����sin��BCQ=![]() =
=![]() ��sin��CBQ=
��sin��CBQ=![]() =
=![]() ����PM=PCsin��PCQ=
����PM=PCsin��PCQ=![]() t��PN=PBsin��CBQ=
t��PN=PBsin��CBQ=![]() ��10��t������
��10��t������![]() t=
t=![]() ��10��t�������t=
��10��t�������t=![]() ��
��
����m=8ʱ��ͬ�������t=![]() �������ı���PMQNΪ������ʱ��t��ֵΪ
�������ı���PMQNΪ������ʱ��t��ֵΪ![]() ��
��![]() ��
��