题目内容
一等腰梯形两组对边中点连线段的平方和为8,则这个等腰梯形的对角长为_ ▲ .
2
此题涉及四边形部分的知识,运用中位线定理来解决。
解答:如图,等腰梯形ABCD,AD∥BC,AB=CD,E、F分别为AB、CD的中点,G、H分别为AD、BC的中点,连接EF,GH交于点O,若EF2+GH2=8,则BD=
解:顺次连接EHFGE,
 ∵E、G分别是AB、AD的中点,F、H分别是CD、BC的中点,
∵E、G分别是AB、AD的中点,F、H分别是CD、BC的中点,
∴EG是△ABD的中位线,FH是△CDB的中位线
∴EG= BD ,FH=
BD ,FH= BD
BD
∴EG=FH= BD
BD
同理可证,EH=GF= AC
AC
∵四边形ABCD是等腰梯形,
∴BD=AC
∴EG=FH=EH=GF
∴四边形EHFG是菱形
∴EF⊥GH,∠EOG=90º;EO= EF,GO=
EF,GO= GH
GH
∴EG= =
= =
=
∵EF2+GH2="8"
∴EG= ×
× =
=
∴BD=2EG=
解答:如图,等腰梯形ABCD,AD∥BC,AB=CD,E、F分别为AB、CD的中点,G、H分别为AD、BC的中点,连接EF,GH交于点O,若EF2+GH2=8,则BD=
解:顺次连接EHFGE,
 ∵E、G分别是AB、AD的中点,F、H分别是CD、BC的中点,
∵E、G分别是AB、AD的中点,F、H分别是CD、BC的中点,∴EG是△ABD的中位线,FH是△CDB的中位线
∴EG=
 BD ,FH=
BD ,FH= BD
BD∴EG=FH=
 BD
BD同理可证,EH=GF=
 AC
AC∵四边形ABCD是等腰梯形,
∴BD=AC
∴EG=FH=EH=GF
∴四边形EHFG是菱形
∴EF⊥GH,∠EOG=90º;EO=
 EF,GO=
EF,GO= GH
GH∴EG=
 =
= =
=
∵EF2+GH2="8"
∴EG=
 ×
× =
=
∴BD=2EG=


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ②△ABF≌△EDF ③
②△ABF≌△EDF ③ ④AD=BD·cos45°正确的是( )
④AD=BD·cos45°正确的是( )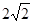 ,CD=
,CD= ,
, ,则点P的个数为【 】
,则点P的个数为【 】

 ㎝2.
㎝2.
