Question

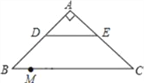
【题目】如图，在Rt△ABC中.∠A=90°.AB=AC，BC=20，DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是_____．

Answer 1

【答案】或．

【解析】试题分析：如图作EF⊥BC于F，DN′⊥BC于N′交EM于点O′，此时∠MN′O′=90°，

∵DE是△ABC中位线，∴DE∥BC，DE=BC=10，∵DN′∥EF，∴四边形DEFN′是平行四边形，∵∠EFN′=90°，∴四边形DEFN′是矩形，∴EF=DN′，DE=FN′=10，∵AB=AC，∠A=90°，∴∠B=∠C=45°，∴BN′=DN′=EF=FC=5，∴，即，解得DO′=．当∠MON=90°时，∵△DOE∽△EFM，∴,根据勾股定理可得EM==13，∴DO=．