题目内容
 如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为
如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为
- A.99
- B.120
- C.143
- D.168
C
分析:首先设GJ的长度为x,则用x分别表示各小正方形的边长,然后根据AD=BC列出关于x的方程,求解方程即可求出x的值,从而可得到AB和BC的长度,进而得到矩形ABCD的面积.
解答:如图:

由题意得正方形FGHI的边长为1,设GJ长度为x,则正方形GJKL的边长为x,正方形LKCM的边长为x,正方形EBJF的边长为x+1,正方形AEIN的边长为x+2,正方形NHMD的边长为x+3.
由于ABCD为矩形,则AD=BC,所以x+2+x+3=x+1+x+x;所以x=4;
AB=x+2+x+1=2x+3=11,BC=3x+1=13,
所以矩形ABCD的面积为:11×13=143.故选C.
点评:本题解题关键是弄清楚各小正方形边长之间的关系.分别用x表示各小正方形的边长,然后利用AD=BC求出x的值,从而得到矩形ABCD的长和宽,进而得到其面积.
分析:首先设GJ的长度为x,则用x分别表示各小正方形的边长,然后根据AD=BC列出关于x的方程,求解方程即可求出x的值,从而可得到AB和BC的长度,进而得到矩形ABCD的面积.
解答:如图:

由题意得正方形FGHI的边长为1,设GJ长度为x,则正方形GJKL的边长为x,正方形LKCM的边长为x,正方形EBJF的边长为x+1,正方形AEIN的边长为x+2,正方形NHMD的边长为x+3.
由于ABCD为矩形,则AD=BC,所以x+2+x+3=x+1+x+x;所以x=4;
AB=x+2+x+1=2x+3=11,BC=3x+1=13,
所以矩形ABCD的面积为:11×13=143.故选C.
点评:本题解题关键是弄清楚各小正方形边长之间的关系.分别用x表示各小正方形的边长,然后利用AD=BC求出x的值,从而得到矩形ABCD的长和宽,进而得到其面积.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
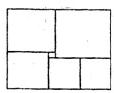 如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为( )
如图所示的矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的面积为( )
 安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
