题目内容
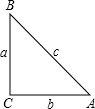 附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=
附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=| a |
| c |
| b |
| c |
| a |
| b |
分析:利用锐角三角函数的概念:sinA=
,cosA=
,tanA=
对(1)sin2A+cos2A=1;(2)用tanA=
进行证明.
| a |
| c |
| b |
| c |
| a |
| b |
| sinA |
| cosA |
解答:解:存在的一般关系有:
(1)sin2A+cos2A=1;
(2)tanA=
.
证明:(1)∵sinA=
,cosA=
,
a2+b2=c2,
∴sin2A+cos2A=
+
=
=
=1.
(2)∵sinA=
,cosA=
,
∴tanA=
=
,
=
.
(1)sin2A+cos2A=1;
(2)tanA=
| sinA |
| cosA |
证明:(1)∵sinA=
| a |
| c |
| b |
| c |
a2+b2=c2,
∴sin2A+cos2A=
| a2 |
| c2 |
| b2 |
| c2 |
| a2+b2 |
| c2 |
| c2 |
| c2 |
(2)∵sinA=
| a |
| c |
| b |
| c |
∴tanA=
| a |
| b |
| ||
|
=
| sinA |
| cosA |
点评:本题通过利用勾股定理和锐角三角函数的概念来对锐角的一般关系:
(1)sin2A+cos2A=1;(2)tanA=
的证明推导.
(1)sin2A+cos2A=1;(2)tanA=
| sinA |
| cosA |

练习册系列答案
相关题目
 ,cosA=
,cosA=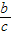 ,tanA=
,tanA= .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.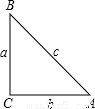
 ,cosA=
,cosA= ,tanA=
,tanA=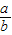 .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.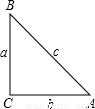
 ,cosA=
,cosA=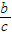 ,tanA=
,tanA= .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
 ,cosA=
,cosA=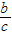 ,tanA=
,tanA=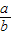 .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.