题目内容
 如图,E、F在双曲线y=
如图,E、F在双曲线y=| k | x |
分析:如图,连接FO,由于S△AME=2,AE=EF,由此得到△AFM的面积,又FM⊥x轴于M,由此得到FM∥y轴,所以得到△FOM的面积和△AFM的面积相等,由此即可求出k值.
解答: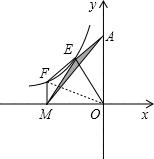 解:如图,连接FO,
解:如图,连接FO,
∵S△AME=2,AE=EF,
∴S△AFM=2S△AME=4,
∵FM⊥x轴于M,
∴FM∥y轴,
∴S△AFM=S△OMF=4,即
×FM×MO=4,FM×MO=8,
又F在双曲线y=
上,
∴k=-8.
故答案为:-8.
 解:如图,连接FO,
解:如图,连接FO,∵S△AME=2,AE=EF,
∴S△AFM=2S△AME=4,
∵FM⊥x轴于M,
∴FM∥y轴,
∴S△AFM=S△OMF=4,即
| 1 |
| 2 |
又F在双曲线y=
| k |
| x |
∴k=-8.
故答案为:-8.
点评:此题主要考查了反比例函数的图象和性质,解题的关键是利用等积变换分别求出相关几个三角形的面积,然后利用面积和反比例函数图象的关系解决问题.

练习册系列答案
相关题目

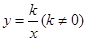 上,点P′(1,2)与点关于
上,点P′(1,2)与点关于 轴对称,则此双曲线的函数表达式为 .
轴对称,则此双曲线的函数表达式为 .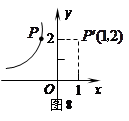
 上,点P′(1,2)与点关于
上,点P′(1,2)与点关于 轴对称,则此双曲线的函数表达式为 .
轴对称,则此双曲线的函数表达式为 .
 上,FE交y轴于A点,AE=EF,FM⊥x轴于M,若S△AME=2,则k= .
上,FE交y轴于A点,AE=EF,FM⊥x轴于M,若S△AME=2,则k= .