题目内容
如图，在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE，∠FAB=∠EAD=90°，
连结AC、EF．在图中找一个与△FAE全等的三角形，并加以证明．
连结AC、EF．在图中找一个与△FAE全等的三角形，并加以证明．
△FAE≌△ABC或△CDA，证明见解析.
试题分析：∵∠BAD+∠EAF+∠FAB+∠EAD=360°，∠FAB=∠EAD=90°，∴∠BAD+∠EAF=180°∵四边形ABCD为平行四边形，∴∠BAD+∠ABC=180°，∴∠EAF=∠ABC（同角的补角相等）∵△ABF和△ADE都是等腰直角三角形，∴AF=AB,AE=AD又∵□ABCD中AD=BC（平行四边形的性质）∴AE=BC
∵在△FAE和△ABC中AF=AB，∠EAF=∠ABC，AE=BC，∴△FAE≌△ABC，又∵四边形ABCD为平行四边形△CDA≌△ABC∴△FAE≌△CDA
练习册系列答案
备战中考寒假系列答案
相关题目
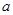，AM=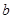
，则CD的长为（ ）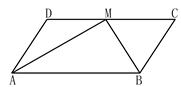
）
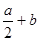
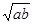
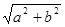
相互外离，它们的半径都是1，顺次连接五个圆心得到五边形ABCDE,则图中五个扇形（阴影）部分的面积之和是多少？
”，那么四边形ABCD一定是平行四边形；
”，那么四边形ABCD一定是平行四边形