题目内容
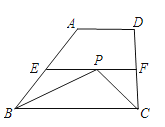
【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

(1)求证:AE∥B′C;
(2)若AB=4,BC=6,求线段B′C的长。
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)过E作EH⊥CF于H,由折叠的性质和点E是BC的中点以及矩形的性质可得△ABE∽△EHC,进而求得∠AEB=∠ECH,最后可得AE∥B′C;
(2)由(1)中的△ABE∽△EHC,即可求得线段B′C的长.
试题解析:
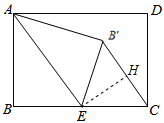
(1)证明:解:过E作EH⊥CF于H,
由折叠的性质得:BE=EF,∠BEA=∠FEA,
∵点E是BC的中点,
∴CE=BE,
∴EB′=CE,
∴∠B′EH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴∠AEB=∠ECH,
∴AE∥B′C;
(2)解:∵△ABE∽△EHC,
∴![]() ,
,
∴HC=![]() =
=![]() .
.

练习册系列答案
相关题目