Question

【题目】如图，抛物线y=ax2+bx+3经过A（﹣3，0），B（﹣1，0）两点．

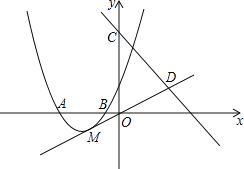
（1）求抛物线的解析式；

（2）设抛物线的顶点为M，直线y=﹣2x+9与y轴交于点C，与直线OM交于点D．现将抛物线平移，保持顶点在直线OD上．若平移的抛物线与射线CD（含端点C）只有一个公共点，求它的顶点横坐标的值或取值范围．

Answer 1

【答案】（1）y=x2+4x+3；（2）h=4，顶点横坐标的取值范围是≤h＜或h=4．

【解析】

试题分析：（1）直接用待定系数法就可以求出抛物线的解析式；

（2）由（1）的解析式求出抛物线的顶点坐标，根据抛物线的顶点坐标求出直线OD的解析式，设平移后的抛物线的顶点坐标为（h，h），就可以表示出平移后的解析式，当抛物线经过点C时就可以求出h值，抛物线与直线CD只有一个公共点时可以得出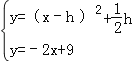，得x2+（﹣2h+2）x+h2+h﹣9=0，从而得出△=（﹣2h+2）2﹣4（h2+h﹣9）=0求出h=4，从而得出结论．

解：（1）抛物线解析式y=ax2+bx+3经过A（﹣3，0），B（﹣1，0）两点，

∴，

解得，

∴抛物线的解析式为y=x2+4x+3．

（2）由（1）配方得y=（x+2）2﹣1，

∴抛物线的顶点坐标为M（﹣2，﹣1），

∴直线OD的解析式为y=x，

于是可设平移后的抛物线的顶点坐标为（h，h），

∴平移后的抛物线的解析式为y=（x﹣h）2+h，

当抛物线经过点C时，∵C（0，9），

∴h2+h=9．

解得h=，

∴当≤h＜时，平移后的抛物线与射线CD只有一个公共点；

当抛物线与直线CD只有一个公共点时，

由方程组，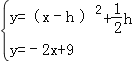

得x2+（﹣2h+2）x+h2+h﹣9=0，

∴△=（﹣2h+2）2﹣4（h2+h﹣9）=0，

解得h=4，

此时抛物线y=（x﹣4）2+2与直线CD唯一的公共点为（3，3），点（3，3）在射线CD上，符合题意．

故平移后抛物线与射线CD只有一个公共点时，顶点横坐标的取值范围是≤h＜或h=4．