题目内容
一个圆桶,底面半径为12cm,高为32cm,则桶内所能容下的最长木棒的长度为
40
40
cm.分析:根据题意画出示意图,AC为圆桶底面直径,AC=24cm,CB=32cm,那么线段AB的长度就是桶内所能容下的最长木棒的长度,在直角三角形ABC中利用勾股定理即可求出AB,也就求出了桶内所能容下的最长木棒的长度.
解答: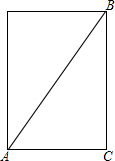 解:如图,AC为圆桶底面直径,
解:如图,AC为圆桶底面直径,
∴AC=2×12=24cm,CB=32cm,
∴线段AB的长度就是桶内所能容下的最长木棒的长度,
∴AB=
=
=40cm.
故桶内所能容下的最长木棒的长度为40cm.
故答案为:40.
 解:如图,AC为圆桶底面直径,
解:如图,AC为圆桶底面直径,∴AC=2×12=24cm,CB=32cm,
∴线段AB的长度就是桶内所能容下的最长木棒的长度,
∴AB=
| AC2+BC2 |
| 242+322 |
故桶内所能容下的最长木棒的长度为40cm.
故答案为:40.
点评:本题考查勾股定理的实际应用,首先要正确理解题意,明白怎么放桶内所能容下的木棒最长,然后灵活利用勾股定理,难度一般.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
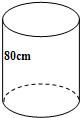 如图,一个圆桶的底面半径为30cm,高为80cm,求桶内能容下的最长的木棒长.
如图,一个圆桶的底面半径为30cm,高为80cm,求桶内能容下的最长的木棒长. 如图,一个圆桶的底面半径为30cm,高为80cm,求桶内能容下的最长的木棒长.
如图,一个圆桶的底面半径为30cm,高为80cm,求桶内能容下的最长的木棒长.