题目内容
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1) 设点P的纵坐标为p,写出p随k变化的函数关系式;
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。
(1) 设点P的纵坐标为p,写出p随k变化的函数关系式;
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于
 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。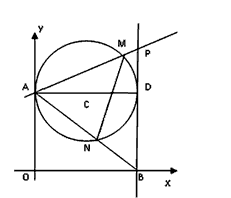
| 解:(1)∵y轴和直线l都是⊙C的切线, ∴OA⊥AD,BD⊥AD, 又∵OA⊥OB, ∴∠AOB=∠OAD=∠ADB=90°, ∴四边形OADB是矩形, ∵⊙C的半径为2, ∴AD=OB=4, ∵点P在直线l上, ∴点P的坐标为(4,p), 又∵点P也在直线AP上, ∴p=4k+3; |
|
| (2)连接DN, ∵AD是⊙C的直径, ∴∠AND=90°, ∵∠AND=90°-∠DAN,∠ABD=90°-∠DAN, ∴∠AND=∠ABD, 又∵∠ADN=∠AMN, ∴∠ABD=∠AMN, ∵∠MAN=∠BAP, ∴△AMN∽△ABP; |
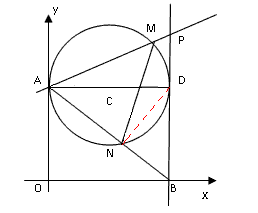 |
|
(3)存在, |

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
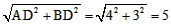 ,
, AB·DN=
AB·DN=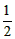 AD·DB,
AD·DB,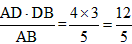 ,
,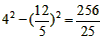 ,
,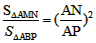
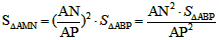 ,
,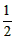 PB·AD=
PB·AD=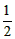 (4k+3)×4=2(4k+3),
(4k+3)×4=2(4k+3), 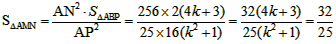 ,
,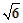 ,k2=2-
,k2=2-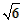 ,
,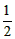 PB·AD=
PB·AD=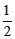 [-(4k+3)]×4=-2(4k+3),
[-(4k+3)]×4=-2(4k+3), 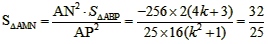 ,
, 或k=-2时,△AMN的面积等于
或k=-2时,△AMN的面积等于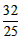 。
。
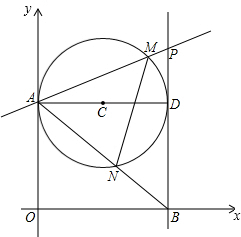 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.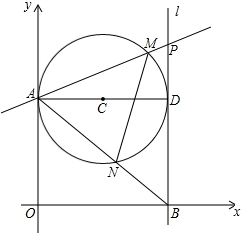 如图,第一象限内半径为4的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+6.
如图,第一象限内半径为4的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+6.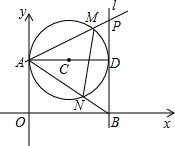 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则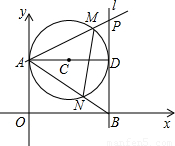 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则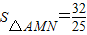 时,k= .
时,k= .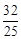 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。