题目内容
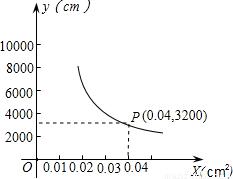
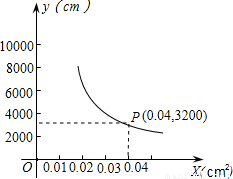
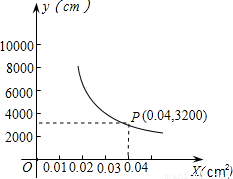
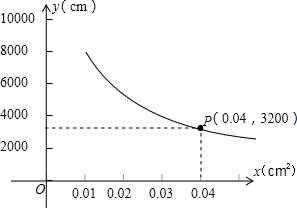 你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数.假设它的图象如图所示.
你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(cm)是面条粗细(横截面积)x(cm2)的反比例函数.假设它的图象如图所示.(1)求y与x的函数关系式.
(2)若面条的横截面积是0.02cm2时,面条的长度是多少cm?
分析:(1)根据反比例函数图象经过点(0.04,3200),利用待定系数法进行解答;
(2)把s=0.02代入函数解析式计算即可求出总长度y的值.
(2)把s=0.02代入函数解析式计算即可求出总长度y的值.
解答:解:(1)设反比例函数图象设解析式为y=
由图得,反比例函数上一点坐标为(0.04,3200)代入y=
,
有3200=
解得k=128,又题中实际意义需x>0.
∴y=
(x>0).
(2)令s=0.02得y=
=6400cm
| k |
| x |
由图得,反比例函数上一点坐标为(0.04,3200)代入y=
| k |
| x |
有3200=
| k |
| 0.04 |
解得k=128,又题中实际意义需x>0.
∴y=
| 128 |
| x |
(2)令s=0.02得y=
| 128 |
| 0.02 |
点评:本题考查了反比例函数的应用,待定系数法求函数解析式,根据图象找出函数图象经过的点的坐标是解题的关键,难度不大.

练习册系列答案
相关题目
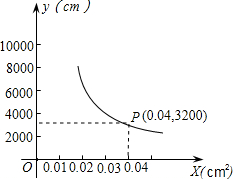 你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度у(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则у与x的函数关系式为
你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度у(cm)是面条粗细(横截面积)x(cm2)的反比例函数,假设其图象如图所示,则у与x的函数关系式为