题目内容
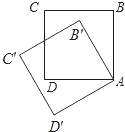如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（ ）A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
分析：此题只需把公共部分分割成两个三角形，根据旋转的旋转发现两个三角形全等，从而求得直角三角形的边，再进一步计算其面积．
解答：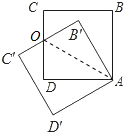
解：设CD与B′C′相交于点O，连接OA．
根据旋转的性质，得∠BAB′=30°，则∠DAB′=60°．
在Rt△ADO和Rt△AB′O中，AD=AB′，AO=AO，
∴Rt△ADO≌Rt△AB′O．
∴∠OAD=∠OAB′=30°．
又AD=1，∴OD=
．
∴公共部分的面积=2×
×
×1=1×
=
．故选D．
解：设CD与B′C′相交于点O，连接OA．根据旋转的性质，得∠BAB′=30°，则∠DAB′=60°．
在Rt△ADO和Rt△AB′O中，AD=AB′，AO=AO，
∴Rt△ADO≌Rt△AB′O．
∴∠OAD=∠OAB′=30°．
又AD=1，∴OD=
| ||
| 3 |
∴公共部分的面积=2×
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评：本题主要考查了利用正方形和旋转的性质来求三角形的面积．
练习册系列答案
相关题目
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
