Question

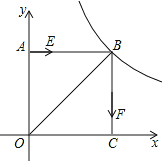
【题目】如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数（x＞0）图象上，△BOC的面积为8．

（1）求反比例函数的关系

（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？

（3）当运动时间为秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）、y=；（2）、S=－+4；（3）、P（，0）

【解析】

试题分析：（1）、设点B的坐标为（a，a），根据三角形的面积得出a的值，然后求出点B的坐标，计算反比例函数的解析式；（2）、根据题意得出AE=t，BF=2t，BE=4－t，然后求出函数解析式；（3）、首先根据t的值求出点E和点F的坐标，作F点关于x轴的对称点，求出直线E的直线解析式，从而得出点P的坐标.

试题解析：（1）、∵四边形AOCB为正方形，

∴AB=BC=OC=OA，

设点B坐标为（a，a），

∵C=8，

∴=8，

∴a=±4

又∵点B在第一象限，

∴点B坐标为（4，4），

将点B（4，4）代入y=得，k=16

∴反比例函数解析式为y=

（2）、∵运动时间为t，

∴AE=t，BF=2t

∵AB=4，

∴BE=4-t，

∴=（4-t）2t=-+4t=-－+4，

（3）、存在．

当t=时，点E的坐标为（，4），点F的坐标为（4，）

作F点关于x轴的对称点，得F1（4，-），经过点E、作直线

由E（，4），（4，-）代入y=ax+b得：

解得：

可得直线E的解析式是y=-2x+

当y=0时，x=

∴P点的坐标为（，0）