题目内容
(本题满分5分)某校九年级两个班各为红十字会捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程.
解法一:求两个班人均捐款各多少元?
设1班人均捐款x元,则2班人均捐款(x+4)元,根据题意得
 ·90%=
·90%= ………………………………………………………(3分)
………………………………………………………(3分)
解得x="36 " 经检验x=36是原方程的根,且符合实际意义………………………(4分)
∴x+4=40 ……………………………………………(5分)
答:1班人均捐36元,2班人均捐40元
解法二:求两个班人数各多少人?
设1班有x人,则根据题意得
 +4=
+4= …………(3分)
…………(3分)
解得x="50" ,经检验x=50是原方程的根,且符合实际意义…(4分)
∴90x % =45 ……………(5分)
答:1班有50人,2班有45人.
(不检验扣1分)解析:
略
设1班人均捐款x元,则2班人均捐款(x+4)元,根据题意得
 ·90%=
·90%= ………………………………………………………(3分)
………………………………………………………(3分)解得x="36 " 经检验x=36是原方程的根,且符合实际意义………………………(4分)
∴x+4=40 ……………………………………………(5分)
答:1班人均捐36元,2班人均捐40元
解法二:求两个班人数各多少人?
设1班有x人,则根据题意得
 +4=
+4= …………(3分)
…………(3分)解得x="50" ,经检验x=50是原方程的根,且符合实际意义…(4分)
∴90x % =45 ……………(5分)
答:1班有50人,2班有45人.
(不检验扣1分)解析:
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本题满分10分)某校举行演讲比赛,选出了10名同学担任评委,并事先拟定
从如下4个方案中选择合理的方案来确定每个演讲者的最后得分:
方案1:所有评委所给分的平均数;
方案2:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余
给分的平均数;
方案3:所有评委所给分的中位数;
方案4:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验,
| 得分 | 3.2 | 7 | 7.8 | 8 | 8.4 | 9.8 |
| 评委人数 | 1人 | 1人 | 1人 | 3人 | 3人 | 1人 |
【小题1】(1)分别按上述4个方案计算这个同学演讲的最后得分;
【小题2】(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.

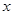 (
(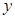 (元)之间的函数关系式.
(元)之间的函数关系式.