题目内容
(1)如图①,在平面直角坐标系xOy中,若点A(-1,3),B(2,-1),则AB=
(用含x1,y1,x2,y2的代数式表示);
(2)如图②,在平面直角坐标系xOy中,点P(x,y)是直线l:y=-
x+2上的一个动点,点M(-1,-1),请你利用题(1)中的结论写出P、M两点的距离d关于点P的横坐标x的函数关系式;
(3)如图③,在(2)的条件下,以M为圆心,单位1长为半径作⊙M,点Q是⊙M上的一个动点,请你利用(2)中的结论,使用配方法,求出PQ的最小值,并求出此时P点的坐标.
5
5
;若A(x1,y1),B(x2,y2),则AB=| (x1-x2)2+(y1-y2)2 |
| (x1-x2)2+(y1-y2)2 |
(2)如图②,在平面直角坐标系xOy中,点P(x,y)是直线l:y=-
| 3 |
| 4 |
(3)如图③,在(2)的条件下,以M为圆心,单位1长为半径作⊙M,点Q是⊙M上的一个动点,请你利用(2)中的结论,使用配方法,求出PQ的最小值,并求出此时P点的坐标.

分析:(1)运用两点间的距离公式即可得出结论;
(2)将P点坐标(x,-
x+2),M点坐标(-1,-1)代入公式即可求解;
(3)配方可得
,根据非负数的性质可得x=
时,d最小,再代入函数关系式求解.
(2)将P点坐标(x,-
| 3 |
| 4 |
(3)配方可得
|
| 4 |
| 5 |
解答:解:(1)AB=
=5,
AB=
;
(2)d=
;
(3)d=
=
.
从上式可知,当x=
时,d最小为3个单位长.
故PQ最短时为3-1=2个单位长,此时点P的坐标为(
,
).
| (-1-2)2+(3+1)2 |
AB=
| (x1-x2)2+(y1-y2)2 |
(2)d=
|
(3)d=
|
|
从上式可知,当x=
| 4 |
| 5 |
故PQ最短时为3-1=2个单位长,此时点P的坐标为(
| 4 |
| 5 |
| 7 |
| 5 |
点评:考查了两点间的距离公式,本题需仔细分析题意,利用公式求解,(3)中最小值可以通过配方法求解.

练习册系列答案
相关题目
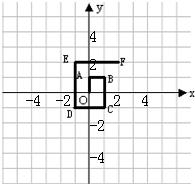 17、如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.①根据图形填表格:
17、如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.①根据图形填表格: