题目内容
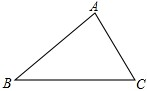
 如图,三边均不等长的△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.判断下列作法何者正确
如图,三边均不等长的△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.判断下列作法何者正确
- A.作中线
 ,再取
,再取 的中点O
的中点O - B.分别作中线
 、
、 ,再取此两中线的交点O
,再取此两中线的交点O - C.分别作
 、
、 的中垂线,再取此两中垂线的交点O
的中垂线,再取此两中垂线的交点O - D.分别作∠A、∠B的角平分线,再取此两角平分线的交点O
B
分析:根据三角形重心的性质,重心到顶点的距离与重心到对边中点的距离之比为2:1,利用三角形面积公式即可解答此题.
解答: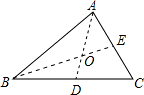 解:别作中线AD、BE,再取此两中线的交点O,
解:别作中线AD、BE,再取此两中线的交点O,
∴O为△ABC的重心,得到AO:OD=2:1,
所以△OBC面积为△ABC面积的1:3,
同理△OAB,△OAC的面积也是△ABC面积的1:3.
∴S△OAB=S△BOC=S△OCA,
∴B正确.
故选B.
点评:此题主要考查学生对三角形的重心和三角形面积等知识点的理解和掌握,难度不大,解答此题的关键是准确掌握三角形重心的定义.
分析:根据三角形重心的性质,重心到顶点的距离与重心到对边中点的距离之比为2:1,利用三角形面积公式即可解答此题.
解答:
 解:别作中线AD、BE,再取此两中线的交点O,
解:别作中线AD、BE,再取此两中线的交点O,∴O为△ABC的重心,得到AO:OD=2:1,
所以△OBC面积为△ABC面积的1:3,
同理△OAB,△OAC的面积也是△ABC面积的1:3.
∴S△OAB=S△BOC=S△OCA,
∴B正确.
故选B.
点评:此题主要考查学生对三角形的重心和三角形面积等知识点的理解和掌握,难度不大,解答此题的关键是准确掌握三角形重心的定义.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
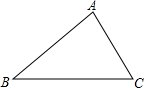 如图,三边均不等长的△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.判断下列作法何者正确( )
如图,三边均不等长的△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.判断下列作法何者正确( )A、作中线
| ||||
B、分别作中线
| ||||
C、分别作
| ||||
| D、分别作∠A、∠B的角平分线,再取此两角平分线的交点O |


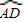 ,再取
,再取 的中点O
的中点O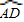 、
、 ,再取此两中线的交点O
,再取此两中线的交点O 、
、 的中垂线,再取此两中垂线的交点O
的中垂线,再取此两中垂线的交点O
 ,再取
,再取 的中点O
的中点O ,
, ,再取此两中线的交点O
,再取此两中线的交点O ,
, 的中垂线,再取此两中垂线的交点O
的中垂线,再取此两中垂线的交点O