题目内容
如图,甲、乙两楼相距50米,从乙楼底望甲楼顶仰角为60°,从甲楼顶望乙楼顶俯角为30°,求两楼的高度.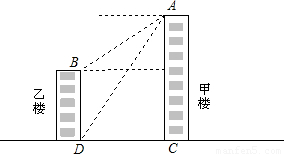
【答案】分析:首先过点B作BE⊥AE于点E,根据题意得:CD=AE=50米,∠EAB=30°,∠ADC=60°,然后在Rt△ABE与Rt△BCD中,用正切函数计算即可求得两楼的高度.
解答:解:过点B作BE⊥AE于点E,
∴∠E=90°,
根据题意得:CD=AE=50米,∠EAB=30°,∠ADC=60°,
在Rt△ABE中,tan∠EAB=tan30°=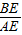 =
= ,
,
∴BE=AE• =50×
=50× =
= ≈29(米),
≈29(米),
在Rt△ACD中,tan∠ADC=tan60°= ,
,
∴AC=CD•tan60°=50×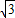 ≈87(米),
≈87(米),
BD=AC-BE=87-29=58(米).
点评:本题考查仰角与俯角的定义,要求学生能借助仰角与俯角构造直角三角形并解直角三角形.注意数形结合思想的应用.
解答:解:过点B作BE⊥AE于点E,
∴∠E=90°,

根据题意得:CD=AE=50米,∠EAB=30°,∠ADC=60°,
在Rt△ABE中,tan∠EAB=tan30°=
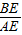 =
= ,
,∴BE=AE•
 =50×
=50× =
= ≈29(米),
≈29(米),在Rt△ACD中,tan∠ADC=tan60°=
 ,
,∴AC=CD•tan60°=50×
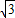 ≈87(米),
≈87(米),BD=AC-BE=87-29=58(米).
点评:本题考查仰角与俯角的定义,要求学生能借助仰角与俯角构造直角三角形并解直角三角形.注意数形结合思想的应用.

练习册系列答案
相关题目
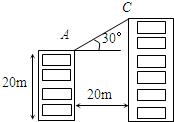 如图,甲、乙两楼相距20m,甲楼高20m,自甲楼顶A看乙楼楼顶C,仰角为30°,则乙楼的高为
如图,甲、乙两楼相距20m,甲楼高20m,自甲楼顶A看乙楼楼顶C,仰角为30°,则乙楼的高为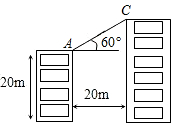 如图,甲、乙两楼相距20m,甲楼高20m,自甲楼顶看乙楼楼顶,仰角为60°,则乙楼的高为
如图,甲、乙两楼相距20m,甲楼高20m,自甲楼顶看乙楼楼顶,仰角为60°,则乙楼的高为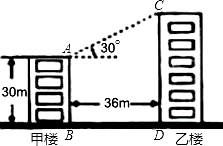 .
.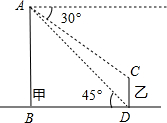 如图,甲,乙两楼相距78m,从甲楼楼顶望乙楼楼顶,俯角为30°,从乙楼楼底望甲楼楼顶仰角为45°,则甲楼的高度为
如图,甲,乙两楼相距78m,从甲楼楼顶望乙楼楼顶,俯角为30°,从乙楼楼底望甲楼楼顶仰角为45°,则甲楼的高度为 楼顶望乙楼顶俯角为30°,求两楼的高度.
楼顶望乙楼顶俯角为30°,求两楼的高度.