题目内容
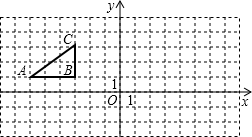
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).(1)将原来的Rt△ABC绕点O顺时针旋转90°得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形.
(2)求线段BC扫过的面积.
(3)求点A旋转到A1路径长.
分析:(1)根据旋转角度、旋转方向、旋转点找出各点的对应点,顺次连接即可得出.
(2)两个扇形的面积相减即可得出线段BC扫过的面积.
(3)根据图形及勾股定理即可算出AA1的长度.
(2)两个扇形的面积相减即可得出线段BC扫过的面积.
(3)根据图形及勾股定理即可算出AA1的长度.
解答:解:(1)所画图形如下: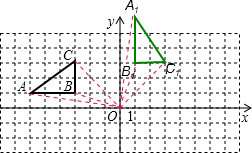
(2)根据图形可得:求线段BC扫过的面积=
π-
π=2π.
(3)根据坐标图可得:AA1=AO×
=
.

(2)根据图形可得:求线段BC扫过的面积=
| 90×OC2 |
| 360 |
| 90×OB2 |
| 360 |
(3)根据坐标图可得:AA1=AO×
| π |
| 4 |
| ||
| 4 |
点评:本题考查旋转作图的知识,综合性强难度较大,关键是正确找出各点的对应点,然后根据坐标图解答各问.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 22、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(2,-1).
22、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(2,-1).
 16、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(-1,0)
16、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(-1,0) 如图,方格纸中的每个小正方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O、M都在格点上.
如图,方格纸中的每个小正方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O、M都在格点上. 如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).