题目内容
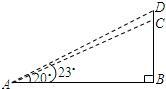
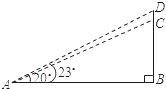如图，山顶建有一座铁塔，塔高CD=30m，某人在点A处测得塔底C的仰角为20°，塔顶D的仰角为23°，求此人距CD的水平距离AB．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin23°≈0.391，cos23°≈0.921，tan23°≈0.424）
分析：首先分析图形：根据题意构造直角三角形；本题涉及多个直角三角形，应利用其公共边构造等量关系，进而可求出答案．
解答：解：在Rt△ABC中，∠CAB=20°，
∴BC=AB•tan∠CAB=AB•tan20°．
在Rt△ABD中，∠DAB=23°，
∴BD=AB•tan∠DAB=AB•tan23°．
∴CD=BD-BC=AB•tan23°-AB•tan20°=AB（tan23°-tan20°）．
∴AB=
≈
=500（m）．
答：此人距CD的水平距离AB约为500m．
∴BC=AB•tan∠CAB=AB•tan20°．
在Rt△ABD中，∠DAB=23°，
∴BD=AB•tan∠DAB=AB•tan23°．
∴CD=BD-BC=AB•tan23°-AB•tan20°=AB（tan23°-tan20°）．
∴AB=
| CD |
| tan23°-tan20° |
| 30 |
| 0.424-0.364 |
答：此人距CD的水平距离AB约为500m．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
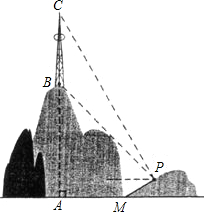如图，山顶建有一座铁塔，塔高BC=80米，测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°，塔顶C点的仰角为60度．已测得小山坡的坡角为30°，坡长MP=40米．求山的高度AB（精确到1米）．（参考数据：
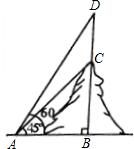如图，山顶建有一座铁塔，塔高CD=20m，某人在点A处，测得塔底C的仰角为45°，塔顶D的仰角为60°，求山高BC（精确到1m，参考数据：
如图，山顶建有一座铁塔，塔高CD=30m，某人在点A处测得塔底C的仰角为20°，塔顶D的仰角为23°，此人距CD的水平距离AB为