题目内容
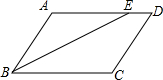 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
求:(1)∠ABE的度数;
(2)DE的长.
解:(1)∵平行四边形ABCD中,∠A=100°
∴∠ABC=180°-∠A=80°
∵∠ABC的平分线交AD于点E
∴∠ABE= ∠ABC=40°.
∠ABC=40°.
(2)在△ABE中,∠AEB=180°-∠ABE-∠A=40°
∴∠AEB=∠ABE=40°
∴AE=AB=3
∴DE=AD-AE=BC-AE=2.
分析:(1)由∠A可得出∠ABC的度数,根据角平分线的定义可得∠ABE的度数;
(2)在△ABE中,根据等角对等边,得AB=AE,根据AD=BC可求DE的长.
点评:本题主要考查了平行四边形的性质,平行四边形的对边平行且相等,灵活运用角平分线的定义求度数是解题的关键.
∴∠ABC=180°-∠A=80°
∵∠ABC的平分线交AD于点E
∴∠ABE=
 ∠ABC=40°.
∠ABC=40°.(2)在△ABE中,∠AEB=180°-∠ABE-∠A=40°
∴∠AEB=∠ABE=40°
∴AE=AB=3
∴DE=AD-AE=BC-AE=2.
分析:(1)由∠A可得出∠ABC的度数,根据角平分线的定义可得∠ABE的度数;
(2)在△ABE中,根据等角对等边,得AB=AE,根据AD=BC可求DE的长.
点评:本题主要考查了平行四边形的性质,平行四边形的对边平行且相等,灵活运用角平分线的定义求度数是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
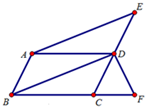 24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2
24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2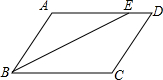 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
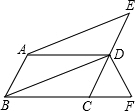 为点F,DF=2
为点F,DF=2