��Ŀ����
����Ŀ����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���O����ͼ��ʽ������һ��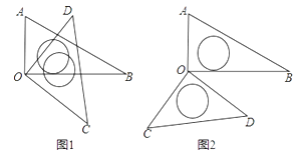
��1����ͼ��1������BOD=35�㣬���AOC�Ķ���������AOC=135�㣬���BOD�Ķ�����
��2����ͼ��2������AOC=140�㣬���BOD�Ķ���
��3�������AOC���BOD�Ĵ�С��ϵ�������ͼ��1��˵�����ɣ�
��4�����dz�AOB�����������dz�COD��OD����OA���غϣ�Ȼ���Ƶ�O��˳ʱ�����ʱ�뷽������ת��һ���Ƕȣ�����AOD��0�㣼��AOD��90�㣩���ڶ��ٶ�ʱ�����������dz߸���һ�����ഹֱ��ֱ��д����AOD�Ƕ����п��ܵ�ֵ������˵������
���𰸡�
��1���⣺����BOD=35�㣬�ߡ�AOB=��COD=90�㣬
���AOC=��AOB+��COD����BOD=90��+90�㩁35��=145�㣬
����AOC=135�㣬
���BOD=��AOB+��COD����AOC=90��+90�㩁135��=45��
��2���⣺��ͼ2������AOC=140�㣬
���BOD=360�㩁��AOC����AOB����COD=40��
��3���⣺��AOC���BOD������
�ߡ�AOD+��BOD+��BOD+��BOC=180�㣮
�ߡ�AOD+��BOD+��BOC=��AOC��
���AOC+��BOD=180�㣬
����ACB���DCE������
��4���⣺OD��ABʱ,��AOD=30��CD��OBʱ,��AOD=45��,
CD��ABʱ,��AOD=75��
OC��ABʱ,��AOD=60
����AOD�Ƕ����п��ܵ�ֵΪ30�㡢45�㡢60�㡢75��
����������1��ץס��֪��ABO�͡�DCO����ֱ�������Σ�����һ�����ݡ�AOC=��AOB+��COD����BOD�����㼴�������AOC�Ķ����������������ݡ�BOC=��DOC-��BOD���ٸ��ݡ�AOC=��BOC+��AOB�����㼴�ɵó���AOC�Ķ���������AOC=135�㣬����һ�����ݡ�BOD=��AOB+��COD����AOC�����㼴�ɵó��𰸣������������ݡ�AOD=��AOC-��DOC���ٸ��ݡ�BOD=��AOB-AOD�����㼴�ɵó��𰸡�
��2���۲�ͼ��2���ɵó���BOD=360�㩁��AOC����AOB����COD������AOC���BOD���������㼴�ɡ�
��3��������֪���ͼ����֤��ACB���DCE������
��4���ֱ����OD��ABʱ��CD��OBʱ��CD��ABʱ��OC��ABʱ�ֱ������AOD�Ķ������ɡ�

 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�