题目内容
 附加题:如图,正方形ABCD正方形ABCD中,BD是对角线,E、F点分别在BC、CD边上,且△AEF是等边三角形.
附加题:如图,正方形ABCD正方形ABCD中,BD是对角线,E、F点分别在BC、CD边上,且△AEF是等边三角形.(1)求证:△ABE≌△ADF;
(2)过点D作DG⊥BD交BC延长线于点G,在DB上截取DH=DA,连接HG.请你参考下面方框中的方法指导,证明:GH=GE.
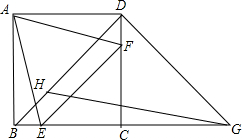
分析:(1)根据HL证明△ABE≌△ADF.
(2)设EC、BE分别为x、y,根据△ABE≌△ADF得出DF=BE、FC=EC;GE=BG-EG,进而用x、y代数式表示出GE2,在Rt△DHG中用x、y的代数式表示出GH2,将表示GE2与GH2的代数式进行整理得出GE=GH.
(2)设EC、BE分别为x、y,根据△ABE≌△ADF得出DF=BE、FC=EC;GE=BG-EG,进而用x、y代数式表示出GE2,在Rt△DHG中用x、y的代数式表示出GH2,将表示GE2与GH2的代数式进行整理得出GE=GH.
解答:证明:(1)∵正方形ABCD,
∴AB=AD.
∵△AEF是等边三角形,
∴AE=AF.
∴△ABE≌△ADF.
(2)设EC=x,BE=y,那么AB=DA=x+y,
∵△ABE≌△ADF,
∴DF=BE.
∴FC=EC.
GE2=(BG-BE)2=(2x+y)2=4x2+4xy+y2=3x2+x2+4xy+y2①
在Rt△ABE中,由勾股定理得:
∴EF=AE=
x,
∵∠BDG=90°,∠DBG=45°,
∴△BDG是等腰Rt△,
在Rt△DHG中,GH2=3DA2=3x2+6xy+3y2
在Rt△ABE中,由勾股定理得:
2x2=(x+y)2+y2,即x2=2xy+2y2②
将②代入①即得:GE2=3x2+6xy+3y2
∴GH=GE.
∴AB=AD.
∵△AEF是等边三角形,
∴AE=AF.
∴△ABE≌△ADF.
(2)设EC=x,BE=y,那么AB=DA=x+y,
∵△ABE≌△ADF,
∴DF=BE.
∴FC=EC.
GE2=(BG-BE)2=(2x+y)2=4x2+4xy+y2=3x2+x2+4xy+y2①
在Rt△ABE中,由勾股定理得:
∴EF=AE=
| 2 |
∵∠BDG=90°,∠DBG=45°,
∴△BDG是等腰Rt△,
在Rt△DHG中,GH2=3DA2=3x2+6xy+3y2
在Rt△ABE中,由勾股定理得:
2x2=(x+y)2+y2,即x2=2xy+2y2②
将②代入①即得:GE2=3x2+6xy+3y2
∴GH=GE.
点评:本题首先计算得出两线段的平方相等,从而得出两线段相等,这是利用代数方法证明几何问题的一个典型例子.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
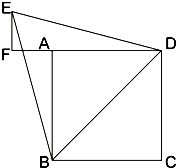 的延长线的垂线EF,垂足为F.
的延长线的垂线EF,垂足为F.

 附加题:如图,正方形ABCD正方形ABCD中,BD是对角线,E、F点分别在BC、CD边上,且△AEF是等边三角形.
附加题:如图,正方形ABCD正方形ABCD中,BD是对角线,E、F点分别在BC、CD边上,且△AEF是等边三角形.